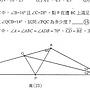
: 想了很久沒有頭緒
: 請教大家 謝謝^^
: 答案:46度
令 CQ 和 AP 交於 D
外角關係可以得到
∠APC = 60 度, ∠QDP = 74 度, ∠ADC = ∠QDP = 74 度, ∠AQC = 30 度
這個 30 度和 60 度給了一個線索, 就是推文的
: → ZO20 : 圓周、圓心角 05/05 16:41
https://i.imgur.com/vJFza8M.png

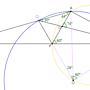
作 △AQC 的外接圓, 設圓心為 O, 連 AO, CO
則 ∠AQC 是這圓的圓周角, 對應的圓心角 ∠AOC = 60 度 = ∠APC
因此 A P O C 四點共圓, 也畫出這個圓出來
再連 PO, 則繼續由圓周角得 ∠AOP = ∠ACP = 28 度
但如果看大圓, 連接 QO, 則同樣由圓周角 ∠ACQ = 14 度得圓心角 ∠AOQ = 28 度
所以這兩個角的 PO / QO 邊其實重合, 也就是 Q-P-O 三點共線
因此由等腰三角形 QOA 中頂角 ∠AOQ 是上面求得的 28 度, 得底角 ∠OQA = 76 度
故所求 ∠PQC = ∠OQC = 76-30 = 46 度 #
--
◢ ˊ_▂▃▄▂_ˋ. ◣ ▅▅ ▅▅ ι●╮ █▄▄▄▄▄
▍./◤_▂▃▄▂_◥ \'▊ HARUHI █████ <■┘ ▄▄▄▄▄▄▄
▎⊿ ◤◤◥█◥◥█Δ ISM By-gamejye ¢|\ ▌▌▌▌▌▄▌▌
▏ζ(▏●‵◥′●▊)Ψ ▏ █ ⊿Δ ▄▄▄ ▄▄▄▄
█/|▊ 〃 、 〃▋ |\ ▎ ハルヒ主義 █▄▄▄█▄▄
◥◥|◣ ‵′ ◢/'◢◢S.O.S 世界を大いに盛り上げるための涼宮ハルヒの団
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 180.177.0.237 (臺灣)
※ 文章網址: https://www.ptt.cc/bbs/Math/M.1620206384.A.500.html
※ 編輯: LPH66 (180.177.0.237 臺灣), 05/05/2021 17:22:01
→
05/05 17:46,
4年前
, 1F
05/05 17:46, 1F
→
05/05 17:46,
4年前
, 2F
05/05 17:46, 2F
討論串 (同標題文章)