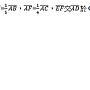Re: [中學]邊長比

看板Math作者LPH66 (信じる力奇跡起こすこと)時間6年前 (2019/12/04 04:04)推噓2(2推 0噓 1→)

留言3則, 2人參與討論串2/3 (看更多)

※ 引述《hightacps (海獺)》之銘言： : https://imgur.com/oAyhImC

: 這題如果用高中向量來解其實不難 : ==> : 向量AD = (1/2)向量AB + (1/2)向量AC : = ?? 向量AE + ?? 向量AF : 接著 : 向量AG = t 向量AD : 即可求解 : 但想請問一下 : 如果是在國中 : 該如何解題呢 : 謝謝用孟氏定理試試看: 延長 EF 和 BC 交於 (右邊很遠的) H 點 (交於右邊的原因是 1/4 > 1/5) E-F-H 切 △BAC 得 (BE/EA)*(AF/FC)*(CH/HB) = 1, 或 (4/1)*(1/3)*(CH/HB) = 1 得 CH:HB = 3:4, 又 D 為 BC 中點, 故 CH:DH:BH = 6:7:8 E-G-H 切 △BAD 得 (BE/EA)*(AG/GD)*(DH/HB) = 1, 或 (4/1)*(AG/GD)*(7/8) = 1 得 AG:GD = 2:7 為第一小題所求 A-F-C 切 △BEH 得 (BA/AE)*(EF/FH)*(HC/CB) = 1, 或 (5/1)*(EF/FH)*(3/1) = 1 得 EF:FH = 1:15 A-G-D 切 △BEH 得 (BA/AE)*(EG/GH)*(HD/DB) = 1, 或 (5/1)*(EG/GH)*(7/1) = 1 得 EG:GH = 1:35 設 EG:GF:FH = x:y:z, 則 (x+y)/z = 1/15, x/(y+z) = 1/35 交叉相乘得 {z = 15(x+y), 下式減上式化簡為 16y = 20x, 即 x:y = 4:5 為第二小題 {y+z = 35x (繼續可以解得 x:y:z = 4:5:135, 這也再度說明 H 點在右邊頗遠的地方) -- LPH [acronym] = Let Program Heal us -- New Uncyclopedian Dictionary, Minmei Publishing Co. -- ※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 180.177.3.123 (臺灣) ※ 文章網址: https://www.ptt.cc/bbs/Math/M.1575403480.A.038.html

推

j0958322080

12/04 08:17, 6年前 , 1^F

12/04 08:17, 1^F

推

aikotoba

12/04 11:57, 6年前 , 2^F

12/04 11:57, 2^F

→

aikotoba

12/04 11:57, 6年前 , 3^F

12/04 11:57, 3^F