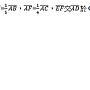看板 [ Math ]
討論串[中學]邊長比
共 3 篇文章
內容預覽： 開啟 | 關閉 | 只限未讀
首頁
上一頁
1
下一頁
尾頁
#3
Re: [中學]邊長比
推噓0(0推 0噓 0→)留言0則，0人參與, 最新作者Vulpix (Sebastian)時間6年前 (2019/12/04 05:09), 編輯資訊
0
1
0
內容預覽:
也可以用面積做。. EG:GF = △AEG:△AGF = △AED:△ADF = 4:5. （因為 5△AED = △ABD = △ADC = 4△ADF）. △ABC = 2△ABD = 10△AED. 而且 △ABC = 20△AEF = 20△AEG*9/4 = 45△AEG. 所以 AG:
(還有17個字)
#2
Re: [中學]邊長比
推噓2(2推 0噓 1→)留言3則，0人參與, 6年前最新作者LPH66 (信じる力 奇跡起こすこと)時間6年前 (2019/12/04 04:04), 編輯資訊
0
1
0
內容預覽:
用孟氏定理試試看:. 延長 EF 和 BC 交於 (右邊很遠的) H 點. (交於右邊的原因是 1/4 > 1/5). E-F-H 切 △BAC 得 (BE/EA)*(AF/FC)*(CH/HB) = 1, 或 (4/1)*(1/3)*(CH/HB) = 1. 得 CH:HB = 3:4, 又 D
(還有557個字)
#1
[中學]邊長比
推噓0(0推 0噓 0→)留言0則，0人參與, 最新作者hightacps (海獺)時間6年前 (2019/12/04 01:25), 編輯資訊
0
1
0
內容預覽:
https://imgur.com/oAyhImC. 這題如果用高中向量來解 其實不難. ==>. 向量AD = (1/2)向量AB + (1/2)向量AC. = ?? 向量AE + ?? 向量AF. 接著. 向量AG = t 向量AD. 即可求解. 但想請問一下. 如果是在國中. 該如何解題呢.
首頁
上一頁
1
下一頁
尾頁