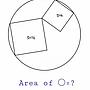
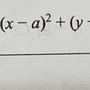Re: [中學] 圓


: : -----
: : Sent from JPTT on my Asus ASUS_Z01RD.
: 這題很繁
: ∠CDO' = a = ∠O'CD
: => ∠CO'O = 2a = 90 - ∠O'OC = 90 - 2∠DBO
: => ∠DBO = 45 - a = ∠BDO
: => ∠BDC = 45 = ∠ADC
: 又因為∠DCA = ∠DEC
: => △DCA ~ △DEC
: DA : DB = 2 : 3
: (2k)^2 + (3k)^2 = 25^2 => k = 25/√13 => 求出DA, DB
: DA * DB = (DA + DB) * CD/√2 => 可求出CD
: CE : 15 = CD : BD
: => CE = 15 CD / BD 可算出一個答案
另解,較簡意作法
R = 25/2
把角度標一標,∠BDC = 45 = ∠ECB
=> ∠CO'E = 90
∠ADC = 45 = ∠CDB
=> OE // AB => DE : BD = r : R
CE = sqrt(2)r
CD為∠D角平分線
DB = 3k, DA = 2k
=> k = 25/sqrt(13) => BD = 3 * 25/sqrt(13)
15^2 = BD [BD - DE] = BD^2 [1 - r/R]
=> CE = sqrt(2) [1 - (15 / BD)^2] R
= sqrt(2) [1 - 13/25] (25/2)
= 6sqrt(2)
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 117.56.175.175
※ 文章網址: https://www.ptt.cc/bbs/Math/M.1543899371.A.628.html
討論串 (同標題文章)