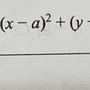[中學] 圓
題目:已知坐標平面上兩點A(3,9)與B(2,1),若直線AB和圓x^2+y^2=10
相交於P、Q兩點,則求 AP/BP + AQ/BQ =?
想法: 這一題可用硬幹法,利用直線AB的參數式,將P、Q作出假設,
代入圓方程式中,但會非常難算,所以想請教是否有其它算法?!
以下是我的想法:
所求= (AP*BQ+AQ*BP)/(BP*BQ)
其中因為A在圓外,B在圓內,
連接BO交圓於兩點,應該可以用內冪性質算出 BP*BQ=5,
且過A作此圓切線,也可以用切割性質求出 AP*AQ=80,
但要套用到所求就會卡住,請高手們解惑,謝謝您 :)
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 61.231.64.160 (臺灣)
※ 文章網址: https://www.ptt.cc/bbs/Math/M.1572967923.A.B38.html
→
11/06 00:10,
6年前
, 1F
11/06 00:10, 1F
推
11/06 01:00,
6年前
, 2F
11/06 01:00, 2F
→
11/06 01:00,
6年前
, 3F
11/06 01:00, 3F
→
11/06 01:01,
6年前
, 4F
11/06 01:01, 4F
→
11/06 01:04,
6年前
, 5F
11/06 01:04, 5F
→
11/06 01:04,
6年前
, 6F
11/06 01:04, 6F
→
11/06 01:06,
6年前
, 7F
11/06 01:06, 7F
→
11/06 08:30,
6年前
, 8F
11/06 08:30, 8F
→
11/06 08:30,
6年前
, 9F
11/06 08:30, 9F
討論串 (同標題文章)