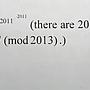Re: [其他] 奧數一題

看板Math作者 (topos)時間7年前 (2018/05/27 02:39), 編輯推噓4(4推 0噓 19→)
留言23則, 4人參與, 7年前最新討論串4/6 (看更多)
令 g(n)=2011^(2011^(.....^2011)) (n個2011) 先證 g(2)=g(3) mod 2013.....(*) pf. 2013=3*11*61 By Euler theorem and CRT, g(1) = g(2) mod [2,10,60] would imply (*). However, 2011^2011 = 2011 mod N, where N=3,4,5 So, g(1)=g(2) mod 60. Hence the result. 因此 g(2011) = g(2010)= ...= g(2) = (-2)^2011=-2^2011=856 mod 2013 提示僅用在最後不用真的去計算 2^2011 mod 2013 -- ※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 118.165.188.189 ※ 文章網址: https://www.ptt.cc/bbs/Math/M.1527359946.A.DF4.html
→
05/29 17:31, 7年前 , 1F
g(1) = g(2) mod [2,10,60]這部分看不懂
05/29 17:31, 1F
推
05/29 20:36, 7年前 , 2F
2013 = 3*11*61, φ(2013) = 2*10*60
05/29 20:36, 2F
→
05/29 20:38, 7年前 , 3F
不過這裡應該不是 CRT... 2 10 60 又不互質
05/29 20:38, 3F
→
05/29 20:40, 7年前 , 4F
這裡應該是 Carmichael(2013) = LCM(2,10,60) = 60
05/29 20:40, 4F
→
05/29 21:06, 7年前 , 5F
後幾行驗證 60 時用 3,4,5 拆開驗才是 CRT
05/29 21:06, 5F
→
05/30 01:08, 7年前 , 6F
no, 對 mod 3,11,31分別用歐拉定理，然後用中國剩餘
05/30 01:08, 6F
→
05/30 01:08, 7年前 , 7F
定理
05/30 01:08, 7F
→
05/30 01:35, 7年前 , 8F
PS. CRT沒有限定兩兩互質
05/30 01:35, 8F
推
05/30 14:32, 7年前 , 9F
我懂了,謝謝.另外我看書上的CRT定理,有說要兩兩互質
05/30 14:32, 9F
推
05/30 16:46, 7年前 , 10F
喔, 是先拆質數再做 CRT...
05/30 16:46, 10F
→
05/30 16:46, 7年前 , 11F
感覺起來這好像差不多是 Carmichael Thm. 的證明?
05/30 16:46, 11F
→
05/30 18:50, 7年前 , 12F
maybe, 但我不記得卡米歇爾定理，我會稱這個過程為"
05/30 18:50, 12F
→
05/30 18:50, 7年前 , 13F
精確的"Euler定理
05/30 18:50, 13F
→
05/30 18:54, 7年前 , 14F
另，只有聯立同餘式之間是consistent, 就可以化簡為
05/30 18:54, 14F
→
05/30 18:54, 7年前 , 15F
mod 互質的同餘式，一般那樣子寫是比較省筆墨。用抽
05/30 18:54, 15F
→
05/30 18:54, 7年前 , 16F
象代數的觀點CRT是 Z/I x Z/J = Z/ (I+J)
05/30 18:54, 16F
推
05/30 19:16, 7年前 , 17F
這樣寫 I, J 還是要 coprime
05/30 19:16, 17F
→
05/30 19:17, 7年前 , 18F
沒有互質條件就只會有單邊的 homomorphism
05/30 19:17, 18F
→
05/30 19:19, 7年前 , 19F
強度上來看, Carmichael Thm 強於 這個精確的 Euler
05/30 19:19, 19F
→
05/30 19:19, 7年前 , 20F
Thm. 本題只需要後者就夠了.
05/30 19:19, 20F
→
05/30 19:20, 7年前 , 21F
Carmichael Thm. 還要求最小, 這裡只需要互質的部分
05/30 19:20, 21F
→
05/30 19:21, 7年前 , 22F
能分開算這個性質.
05/30 19:21, 22F
→
05/31 15:23, 7年前 , 23F
而且右邊要改成Z/(IJ) 或 Z/(I∩J). 難怪覺得怪怪的
05/31 15:23, 23F
‣ 更多 Sfly 的文章
文章代碼(AID): #1R2QdAtq (Math)
‣ 更多 Sfly 的文章
文章代碼(AID): #1R2QdAtq (Math)