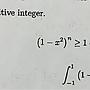Re: [微積] 研究所考古題

: a小題我是令(-x^2)=y在用伯努立不等式證不知道對不對
Thm. 若 n 為正整數, x≧-1, 則 (1+x)^n≧1+nx
Proof.
若 1+nx < 0, 則原式成立
若 1+nx ≧ 0, 由算幾不等式
1+...+1+(1+nx)
1+x = ---------------- ≧ (1*...*1*(1+nx))^(1/n)
n
=> (1+x)^n ≧ 1+nx
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 140.122.136.81
※ 文章網址: https://www.ptt.cc/bbs/Math/M.1486392673.A.1E9.html
※ 編輯: XII (140.122.136.81), 02/06/2017 22:51:47
討論串 (同標題文章)