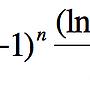Re: [微積] 級數收斂
※ 引述《djljing (娛樂金魚眼)》之銘言:
: Σ(lnn)^2/n^3
: 如何用limit comparison test 判斷收斂?
(L'Hospital's rule)
(ln n)^2/n^3 (ln n)^2 2(ln n)(1/n) 2(ln n)
lim ------------- = lim ----------- = lim -------------- = lim --------
n→∞ 1/n^2 n→∞ n n→∞ 1 n→∞ n
2/n
(L'Hospital's rule) = lim -------
n→∞ 1
= 0
by limit comparison test, Σ(ln n)^2/n^3 和 Σ1/n^2 同歛散
又Σ1/n^2 為p級數 p = 2 case, 收斂
故Σ(ln n)^2/n^3 亦收斂,證畢
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 36.230.20.121
※ 文章網址: https://www.ptt.cc/bbs/Math/M.1448170075.A.496.html
推
11/22 13:41, , 1F
11/22 13:41, 1F
推
11/23 09:50, , 2F
11/23 09:50, 2F
討論串 (同標題文章)