Re: [中學] 空間
※ 引述《xy210742 (Sam)》之銘言:
: 題目:正立方體ABCD-EFGH的邊長6 若P為對角線AG上任一點 求PBD面積最小值
: 請問這題該如何解呢
: 謝謝大大解惑
由於對稱性, 無論 P 在哪裡都有 BP = DP
因此 PDB 一定是等腰三角形, 又 BD 長度固定, 故腰 BP 越短 PDB 面積越小
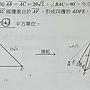
為求 BP 最小值, 考慮長方形 ABGH 這個切面, P 依然是 AG 上一點
可以看到 BP 長度最小值是 BP 垂直 AG, 即 BP 為直角角形 ABG 斜邊上的高時
直角三角形 ABG 中兩股為 AB=6 及 BG=6√2, 斜邊為 AG=6√3
故斜邊上的高 = 6√2/√3 = 2√6, 這即是 BP 最小值
回到原題, 於是所求為底 6√2, 兩腰 2√6 的等腰三角形面積, 易求得為 6√3 #
--
1985/01/12 三嶋鳴海 1989/02/22 優希堂悟 1990/02/22 冬川こころ 1993/07/05 小町
つぐみ 歡迎來到 1994/05/21 高江ミュウ 1997/03/24 守野いづみ 1997/03/24 伊野瀬
チサト 1998/06/18 守野くるみ 打越鋼太郎的 1999/10/19 楠田ゆに 2000/02/15 樋口遙
2002/12/17 八神ココ 2011/01/11 HAL18於朱倉岳墜機 ∞與∫的世界 2011/04/02 茜崎空
啟動 2012/05/21 第貮日蝕計畫預定 2017/05/01~07 LeMU崩壞 2019/04/01~07 某大學合宿
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 123.195.39.85
※ 文章網址: https://www.ptt.cc/bbs/Math/M.1430034454.A.77C.html
討論串 (同標題文章)