Re: [中學] 空間

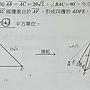
: 請問這樣的條件可以解出來?
設△ABC邊長為k
將正三角形最低的一點移到平面E上
例外二點到平面E的距離為x, y,設x < y
若x < y - x < y
則k^2 - y^2 = 4, k^2 - (y - x)^2 = 9, k^2 - x^2 = 12
=> 4 + y^2 = 9 + (y - x)^2 = 12 + x^2
=> x(2y - x) = 5,y(y - 2x) = 3
令t = y/x可得5t^2 - 16t + 3 = 0 => t = 3
=> y = 3x => x = 1 => △ABC邊長為√13
若y - x < x < y
則k^2 - y^2 = 4, k^2 - x^2 = 9, k^2 - (y - x)^2 = 12
=> 4 + y^2 = 9 + x^2 = 12 + (y - x)^2
一樣得到△ABC邊長 = √13
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 61.231.40.225 (臺灣)
※ 文章網址: https://www.ptt.cc/bbs/Math/M.1711199793.A.AB6.html
推
03/23 23:25,
1年前
, 1F
03/23 23:25, 1F
討論串 (同標題文章)