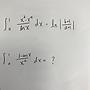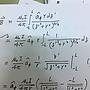Re: [微積] 積分問題
※ 引述《p0poc0la (批林批歐西林欸婁欸)》之銘言:
: 各位好,求版上積分神人..
: (1)
: http://ppt.cc/ErHI
: (2)
: http://ppt.cc/ZASu
: (3)
: http://ppt.cc/ldId
: 拜託了,謝謝大恩大德!
4/√3 √(t^2 - 4 )
原 = ∫ ------------ dt
4 t^3
(1) t^2 - 4 = x^2
t = (x^2 + 4)^(1/2)
dt = x * ( x^2 + 4 )^(-1/2)
2/√3 x^2
∫ -------------- dx ( x = 2tan y )
2√3 (x^2 + 4)^2
2
π/6 4 tan y 2
= ∫ ---------------- * 2 sec y dy
π/3 4
16 sec y
y sin(2y) π/6
= ----- - ------- |
4 8 π/3
- π
= ------
24
(3) ∫ exp(2x) sin(3x) = Im [ ∫ exp(2x) exp(3ix) ]
exp(2x)
= Im [ ---------- ( cos(3x) + isin(3x) ] + C
2 + 3i
1
= exp(2x) * ----- ( 2 sin(3x) - 3 cos(3x) ) + C
13
有錯還請不吝指正。
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 114.45.88.96
※ 文章網址: http://www.ptt.cc/bbs/Math/M.1404183430.A.D5E.html
※ 編輯: a016258 (140.114.137.240), 07/01/2014 14:18:18
推
07/01 16:31, , 1F
07/01 16:31, 1F
→
07/01 16:31, , 2F
07/01 16:31, 2F
推
07/01 16:33, , 3F
07/01 16:33, 3F
→
07/01 17:12, , 4F
07/01 17:12, 4F
→
07/02 09:35, , 5F
07/02 09:35, 5F
討論串 (同標題文章)