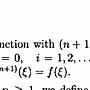Re: [分析] 一題高微
※ 引述《comfiture (永和好地方)》之銘言:
: http://www.lib.ntu.edu.tw/exam/graduate/98/98047.pdf
: A這題
: 我用了球座標後,能夠把 l x-a l 代換掉
: 但卻無法處理好積分範圍
: 所以麻煩版上高手了
: 先謝囉!
不失一般性令 a = (0,0,1)
以球座標表示為 ∫∫∫ e^√(1+r^2-2rcosθ) (r^2 sinθ) dθdr dφ
代換 t = √(1+r^2-2rcosθ), t dt = rsinθ dθ
∫∫∫ e^√(1+r^2-2rcosθ) (r^2 sinθ) dθdr dφ = ∫∫∫ e^t t dt r dr dφ
[ 範圍 θ: 0~π → t : (1-r)~(1+r) ]
= ∫∫ [r e^(1+r) + r e^(1-r)] r dr dφ [ 範圍 r: 0~1 ]
= ∫(e^2 - 5) dφ = 2π(e^2 - 5)
--
※ 發信站: 批踢踢實業坊(ptt.cc)
◆ From: 42.74.0.243
推
02/11 13:34, , 1F
02/11 13:34, 1F
→
02/11 13:34, , 2F
02/11 13:34, 2F
→
02/11 14:02, , 3F
02/11 14:02, 3F
推
02/11 17:05, , 4F
02/11 17:05, 4F
討論串 (同標題文章)