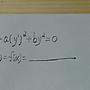Re: [微積] 微分方程
※ 引述《kevin70636 (Bryan)》之銘言:
: y'=((2x+y-1)/(x-2))^2
: 要怎麼解??
: 想了好久~"~
dy y+3 2
---- = (2 + -----)
dx x-2
y+3
令 ----- = u => y = ux - 2u - 3 => dy = udx + xdu - 2du
x-2
2
u dx + 4udx + 4dx = udx + xdu - 2du
2
(u + 3u + 4)dx = (x-2)du
du dx
---------------- = -----
2 x-2
(u+1.5) + 1.25
2 √5
令 ---(u+1.5) = v => du = ----dv
√5 2
2 dv dx
--- -------- = -----
√5 v^2 + 1 x-2
2 -1
=> --- tan v = ㏑(x-2) + ㏑c
√5
2
---(u+1.5) = tan{㏑[c(x-2)]^(√5/2)}
√5
√5
=> y = (x-2){---{tan{㏑[c(x-2)]^(√5/2)}}-1.5} - 3
2
--
※ 發信站: 批踢踢實業坊(ptt.cc)
◆ From: 114.34.133.34
推
11/13 23:10, , 1F
11/13 23:10, 1F
→
11/13 23:12, , 2F
11/13 23:12, 2F
討論串 (同標題文章)