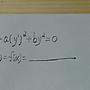[微積] 微分方程
題目是exp(x)dx+[exp(x)cot(y)+2ycsc(y)]dy
if [u(x)M]對y偏微分=[u(x)N]對x偏微分
du/dx=(M對y偏微分-N對x偏微分)u/N
du/u=(M對y偏微分-N對x偏微分)dx/N
ln(u)=-S exp(x)cot(y)/[exp(x)cot(y)+2ycsc(y)] dx
u=[exp(x)cot(y)+2ycsc(y)]^(-1)
算到這邊代回[u(x)M]對y偏微分=[u(x)N]對x偏微分
發現是錯的
但是看了半天
找不到錯在哪裡
麻煩大家指點
--
因為要改的壞習慣太多了 所以就改天吧
--
※ 發信站: 批踢踢實業坊(ptt.cc)
◆ From: 210.66.168.55
→
10/04 03:15, , 1F
10/04 03:15, 1F
→
10/04 03:15, , 2F
10/04 03:15, 2F
推
10/04 10:53, , 3F
10/04 10:53, 3F
→
10/04 10:54, , 4F
10/04 10:54, 4F
→
10/04 10:55, , 5F
10/04 10:55, 5F
討論串 (同標題文章)