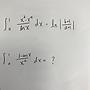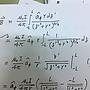[微積] 積分問題

看板Math作者 (大風起兮雲飛揚)時間14年前 (2011/05/21 20:06), 編輯推噓5(5推 0噓 12→)
留言17則, 5人參與, 最新討論串12/74 (看更多)
a和r是constant 2π dθ ∫ ---------------------- 0 a^2 + 2arcosθ + r^2 其實是pde遇到的問題 我把下面換成(a+rcosθ)^2 + r^2 (sinθ)^2 還是沒辦法用1+(tanφ)^2做 可是老師說的好像是分母不管是1還是cos or sin都可以輕易積出來 請問該怎麼做呢 謝謝 -- ※ 發信站: 批踢踢實業坊(ptt.cc) ◆ From: 61.224.43.143
推
05/21 21:34, , 1F
變數變換: cosθ=[1+tan(θ/2)^2]/[1-tan(θ/2)^2]
05/21 21:34, 1F
→
05/21 21:36, , 2F
打反了:cosθ=[1-tan(θ/2)^2]/[1+tan(θ/2)^2]
05/21 21:36, 2F
→
05/21 21:36, , 3F
再令 tan(θ/2) = t
05/21 21:36, 3F
推
05/21 23:51, , 4F
如果會複變的話可以令z=cosθ+isinθ
05/21 23:51, 4F
→
05/21 23:51, , 5F
可以轉換成單位元的線積分,然後再用留數定理
05/21 23:51, 5F
→
05/22 01:56, , 6F
會複變 但不是很明白J大的意思是要我積什麼
05/22 01:56, 6F
→
05/22 01:57, , 7F
應該說z要放在哪邊
05/22 01:57, 7F
→
05/22 02:16, , 8F
我猜他應該是要講Cauchy積分公式<=>Poisson積分公式
05/22 02:16, 8F
推
05/22 09:46, , 9F
z=cosθ+isinθ => cosθ=(z+z^{-1})/2
05/22 09:46, 9F
→
05/22 09:47, , 10F
dz=iexp(iθ)dθ dθ=-iz^{-1}dz
05/22 09:47, 10F
推
05/22 09:53, , 11F
然後整個式子會變成 線積分 |z|=1
05/22 09:53, 11F
→
05/22 09:54, , 12F
int {1/[a^2+2ar(z+z^(-1)/2)+r^2]}*-iz^(-1)dz
05/22 09:54, 12F
→
05/22 19:18, , 13F
感謝j大 這招超級好用的!!!
05/22 19:18, 13F
→
05/22 19:19, , 14F
之前完全沒想到 複變都唸到狗身上去了XD
05/22 19:19, 14F
→
05/22 19:26, , 15F
我今天試著算過這題,似乎再用留數定理的時候會用到
05/22 19:26, 15F
→
05/22 19:27, , 16F
a和r的大小關係,所以可能跟你的PDE有點關聯(吧!?)
05/22 19:27, 16F
推
05/23 15:41, , 17F
= 2π/(a^2 - r^2)
05/23 15:41, 17F
‣ 更多 pobm 的文章
文章代碼(AID): #1DrwhZJh (Math)
討論串 (同標題文章)
完整討論串 (本文為第 12 之 74 篇)：
排序： 最新先 | 最舊先 | 留言數
在新視窗開啟完整討論串 (共74篇)
‣ 更多 pobm 的文章
文章代碼(AID): #1DrwhZJh (Math)