看板
[ Math ]
討論串[中學] 高中數學競賽試題(兩題)
共 3 篇文章
首頁
上一頁
1
下一頁
尾頁
內容預覽:
注意到 t-[t/π]π 其實就只是「t 除以π的『餘數』」. 以及 |sin t| 的週期也是 π. 因此可以知道在一個長度為π的週期裡. x 是一個常數減去 2cos, y 是 2sin. 由於 |sin t| 的週期性, 實際上的角度也可以當成是「t 除以π的『餘數』」. 所以這 cos 和
(還有953個字)
內容預覽:
1.根據中國剩餘定理,原題目等於考慮(a,b)這樣的數對有幾種. 其中a是mod 2的餘數 b是mod 101的餘數. 從f(x)=x(x-37)+5,可以知道mod 2的餘數一定是1. 所以題目可以再簡化成mod 101的餘數有幾種(好處是質數比較好討論). f(x)=f(y) (mod 101)
(還有184個字)
內容預覽:
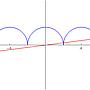
1.設f(x)=x^2-37x+5,將f(1),f(2),......f(202)分別除以202,. 共有幾種可能的相異餘數?. 2.若直線 y = (1/m)x 與. x = 4[t/π]-2cos(t-[t/π]π),t屬於實數. 曲線 {. y = 2|sint|. 共有101個相異交點,其中
(還有10個字)
首頁
上一頁
1
下一頁
尾頁