[中學] 三角形面積問題

看板Math作者 (我喜歡)時間7月前 (2025/06/15 20:06), 編輯推噓1(1推 0噓 24→)
留言25則, 6人參與, 6月前最新討論串4/4 (看更多)
https://i.imgur.com/mAlpWm0.jpeg
https://i.imgur.com/ItmKXAo.jpeg
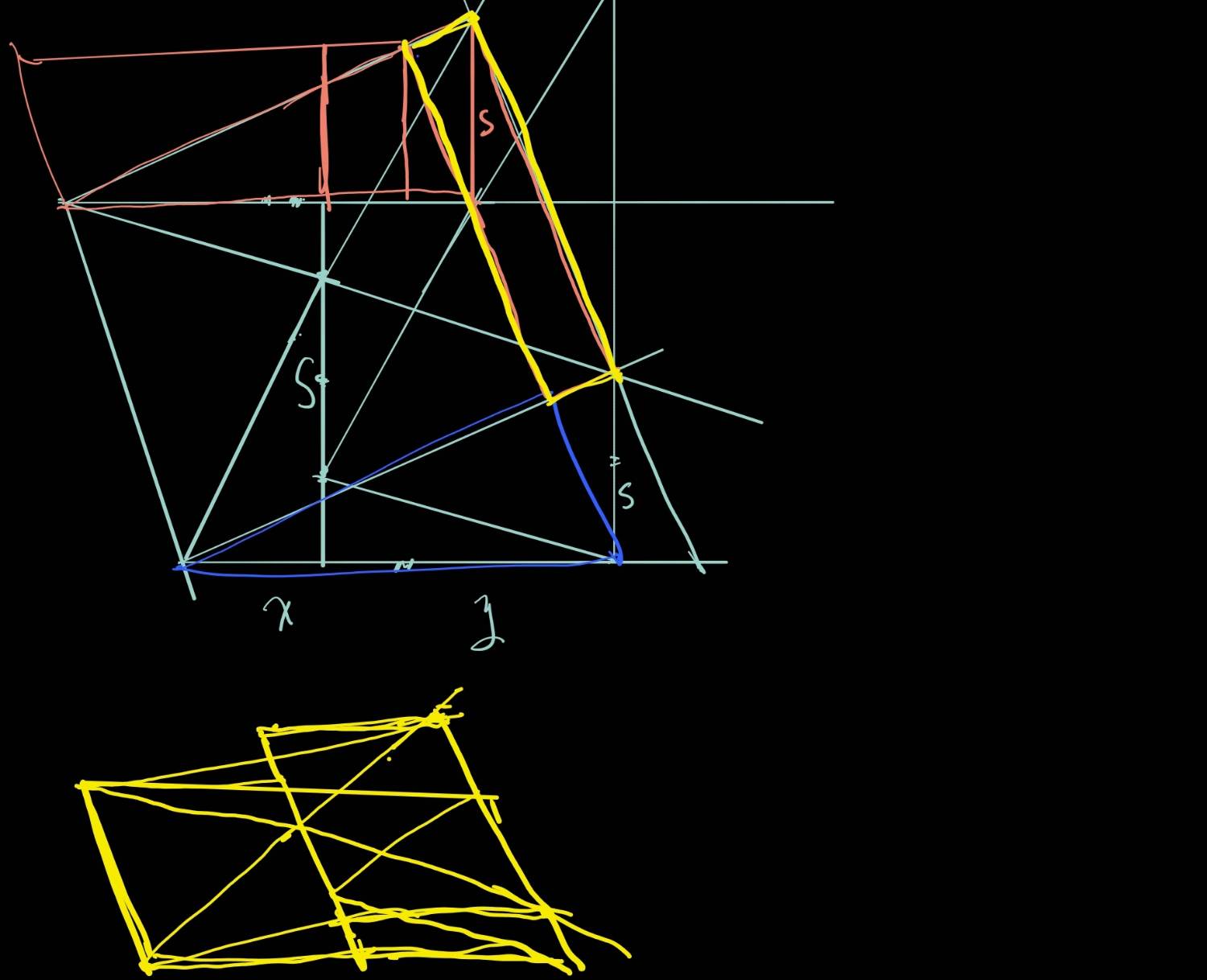
想到的是 如果設梯形的高=h 「F是AB的中點」 利用全等移到左下方 和下方的三角形合起來 [(x+y)乘以1/2h]再除以2 等於整塊梯形的一半 https://i.imgur.com/s1uxH8t.jpeg
1.此題跟上題的模式很像 中間AEF的面積 請問可否用上題的模式 推得是10+6=16？ 2.如果可以 這題「F不是CD的中點」 請問要怎麼證明 AFE或是(10+6) 是梯形ADCE的一半？ 請各位大大幫忙 謝謝 -- ※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 101.9.198.245 (臺灣) ※ 文章網址: https://www.ptt.cc/bbs/Math/M.1749989205.A.151.html
→
06/15 20:45, 7月前 , 1F
如果只論這些條件，那6+8也是同樣的地位
06/15 20:45, 1F
→
06/15 20:45, 7月前 , 2F
所以只是剛好F是中點而已
06/15 20:45, 2F
→
06/15 20:45, 7月前 , 3F
不是中點就不能用，題目沒說就不能假設是中點
06/15 20:45, 3F
→
06/15 20:46, 7月前 , 4F
所以不能預設立場，2的說法都不能成立
06/15 20:46, 4F
→
06/15 20:46, 7月前 , 5F
乖乖算就好了
06/15 20:46, 5F
→
06/15 21:37, 7月前 , 6F
可以證明F剛好是中點，但是還不如直接算
06/15 21:37, 6F
→
06/15 23:53, 7月前 , 7F
請問m大要怎麼證明F是中點?
06/15 23:53, 7F
→
06/16 01:30, 7月前 , 8F
如果作圖的話，除非兩對邊都平行（平行四邊形），
06/16 01:30, 8F
→
06/16 01:34, 7月前 , 9F
以證明中點時平分面積的思路去複製一個反過來的相同
06/16 01:34, 9F
→
06/16 01:35, 7月前 , 10F
梯形，再將這個梯形往上平移使得兩個三角形對頂，
06/16 01:35, 10F
→
06/16 01:36, 7月前 , 11F
則這時可以得到一個新的平行四邊形，且三角形平分
06/16 01:36, 11F
→
06/16 01:37, 7月前 , 12F
面積（因為是中點） 再去比較新舊平行四邊形，可以
06/16 01:37, 12F
→
06/16 01:38, 7月前 , 13F
發現除非平移S為0，不然會有厚度不是0的平行四邊形
06/16 01:38, 13F
→
06/16 01:38, 7月前 , 14F
面積無法抵銷
06/16 01:38, 14F
→
06/16 01:45, 7月前 , 15F
像這樣
06/16 01:45, 15F
→
06/16 01:46, 7月前 , 16F
上面的黃色沒東西抵銷 下面那坨黃色是平行狀況
06/16 01:46, 16F
→
06/16 01:53, 7月前 , 17F
不過其實直接算三角形的高知道跟中點時不同就可知
06/16 01:53, 17F
→
06/16 01:53, 7月前 , 18F
不可能平分面積了
06/16 01:53, 18F
→
06/16 13:50, 7月前 , 19F
令BE=aBC, DE=bDC, a:b=4:5
06/16 13:50, 19F
→
06/16 13:52, 7月前 , 20F
設a=4k,b=5k, (1-4k)(1-5k)=3k
06/16 13:52, 20F
→
06/16 13:53, 7月前 , 21F
k=1/2 or 1/10 (1/2不合）
06/16 13:53, 21F
→
06/16 13:53, 7月前 , 22F
a=4k=2/5, b=5k=1/2
06/16 13:53, 22F
→
06/16 15:36, 6月前 , 23F
謝謝,了解了
06/16 15:36, 23F
推
06/16 22:27, 6月前 , 24F
其實有公式
06/16 22:27, 24F
→
06/20 11:25, 6月前 , 25F
謝謝各位前輩大大解答
06/20 11:25, 25F
‣ 更多 shne21 的文章
文章代碼(AID): #1eJhTL5H (Math)
‣ 更多 shne21 的文章
文章代碼(AID): #1eJhTL5H (Math)