Re: [中學] 國中圓單元求解
※ 引述《helloboy (小悟)》之銘言:
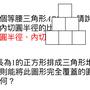
用6個邊長為1的正方形排成三角形堆垛(如圖),
則能將此圖形完全覆蓋的圓,其半徑最小為何?
一開始的想法是圖形對稱,此圓會通過四點,想利用座標化解決,但算出來的半徑不是答案。
想詢問是不是想錯方向了?應該怎麼做?
https://i.imgur.com/NtEYeiJ.jpeg

-----
Sent from JPTT on my iPhone
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 27.242.94.26 (臺灣)
※ 文章網址: https://www.ptt.cc/bbs/Math/M.1734959444.A.F69.html
→
12/23 21:19,
12/23 21:19
→
12/23 21:22,
12/23 21:22
→
12/23 21:50,
12/23 21:50
推
12/23 21:59,
12/23 21:59
→
12/24 01:47,
12/24 01:47
→
12/24 01:47,
12/24 01:47
提供除了座標化以外的兩種做法計算外接圓半徑:
1. 正弦定理
考慮堆垛的
(1) 最上層左上頂點
(2) 最上層右上頂點
(3) 最下層左下頂點
這樣的三角形(就是mantour大說的三角形),也是musicbox說的兩種可能其中之一
(1)-(2): 1
(1)-(3): sqrt(10)
(2)-(3): sqrt(13)
正弦定理說:
a/sin(A) = 2R
考慮(2)為角A
sin(A) = 3/sqrt(13)
sqrt(10)/sin(A) = sqrt(130)/3 = 2R
R = sqrt(130)/6
2.
考慮堆垛的上緣為第一弦,弦長1
考慮堆垛的下緣為第二弦,弦長3
基於弦、半徑與圓心關係,我們知道
令圓心距離第一弦距離x
R^2 = 0.5^2 + x^2 = 1.5^2 + (3-x)^2
整理得到
R^2 - x^2 = 0.25 = 2.25 + 9 - 6x
考慮最後一個等式,得到
x = 11/6
因此
R^2 = 9/36 + 121/36 = 130/36
R = sqrt(130)/6
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 211.23.191.211 (臺灣)
※ 文章網址: https://www.ptt.cc/bbs/Math/M.1735007547.A.98E.html
討論串 (同標題文章)
完整討論串 (本文為第 2 之 2 篇):