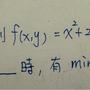Re: [中學] 雙變數函數求極值
f(x, y) = x^2 + 2xy + 3y^2 + 4x + 5y + 6
▽f(x, y) = (f對x偏微分, f對y偏微分)
= (2x + 2y + 4, 2x + 6y + 5)
找f(x,y) 的 Critical point 臨界點
令▽f(x, y) = 0
計算 假如梯度等於零的時候,(x, y) = ?
得到 2x + 2y + 4 = 0
2x + 6y + 5 = 0
解得 (x, y) = (-7/4, -1/4)
用判別式判斷
D = | fxx fxy | = | 2 2 | = 12 - 4 = 8 > 0 臨界點附近圖形開口向上
| fyx fyy | | 2 6 |
fxx > 0
臨界點 (x, y) = (-7/4, -1/4) 有f(x, y)最小值
把(x, y) = (-7/4, -1/4) 代回去原式,得到 最小值 = 15 / 8
※ 引述《weiger1 (您的個人資料)》之銘言:
https://i.imgur.com/UmzmJVL.jpeg

想請問想法,不知如何下手
不好意思題目已修正
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 39.10.8.246 (臺灣)
※ 文章網址: https://www.ptt.cc/bbs/Math/M.1727340351.A.947.html
→
09/26 17:00,
09/26 17:00
※ 編輯: weiger1 (39.10.8.246 臺灣), 09/26/2024 17:14:18
推
09/26 17:31,
09/26 17:31
推
09/26 17:37,
09/26 17:37
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 114.37.222.72 (臺灣)
※ 文章網址: https://www.ptt.cc/bbs/Math/M.1727344112.A.2F0.html
討論串 (同標題文章)
完整討論串 (本文為第 2 之 2 篇):