[微積] 一些關於端點微分判斷的正確觀念

看板Math作者 (God of Computer Science)時間7年前 (2018/10/11 00:23), 7年前編輯推噓6(6推 0噓 28→)
留言34則, 4人參與, 7年前最新討論串1/2 (看更多)
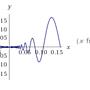
各位板友好，洨弟好久沒在板上發文ㄌ，是說洨弟這學期續接了微積分助教， 為了生活費接下批改作業的重責大任，遇到了一些問題，主要關於端點微分判斷。 當然直接套定義可以很簡單算，可是初學者會用一些旁門左道作答。 先拿一個題目當開場白： 給定 f(x) = x^2 * sin(1/x) if x =\= 0, = 0 if x = 0， https://imgur.com/8vkIXJD
請問 f'(0) 存不存在？ 這題答案是存在的，當然套定義可以簡單看出，因為右導左導都是 0。 可是如果對 x^2 * sin(1/x) 作 chain rule 會發現 f'(0+) 和 f'(0-) 都會震盪。 這很不直覺，明明不管多靠近都會震盪，最後微分卻會變成 0。 不知道針對這個問題是不是有直觀解釋？這是我第一個問題。 接下來是問 f(x) = x * |x| 在 x = 0 可不可以微分？ 答案是可以，卻有人用 f'(0+) = f'(0-) = 0 且 f 在 x = 0 連續來解釋。 不知道這樣解釋可ㄅ可以？ 總之，我想弄清楚判斷端點 x = a 微分與 f'(a+)、f'(a-) 之間的關係。 微分存在 <==> f+'(a) 與 f-'(a) 相等且存在，這是已知的定義。 那麼，f 在 x = a 連續且 f'(a+) 與 f'(a-) 存在且相等 or 不存在 <==> 微分存在， 這句話對不對ㄋ～ 可以靠定義證明ㄇ 這是我第二個問題。 有正確回答第一個或第二個問題的板友前三名各可獲得每題最多 250P， 若沒有滿三名，剩下的獎金會回流給優先完整回答ㄉ板友， 也就是說我至多會貢獻出 250P * 2 * 3 = 1500P，跪求眾板友解答 R ～ -- ※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 140.112.218.7 ※ 文章網址: https://www.ptt.cc/bbs/Math/M.1539188580.A.181.html ※ 編輯: alan23273850 (140.112.218.7), 10/11/2018 00:27:33
推
10/11 01:25, 7年前 , 1F
第一個問題x^2 * sin(1/x)在x=0處f'(0)存在且為0是
10/11 01:25, 1F
→
10/11 01:25, 7年前 , 2F
因為人工加了f(0)=0 as x=0
10/11 01:25, 2F
→
10/11 01:26, 7年前 , 3F
如果只有x^2 * sin(1/x) 是不包含x=0的 所以f'(x)真
10/11 01:26, 3F
→
10/11 01:27, 7年前 , 4F
正要寫為2xsin(1/x)-cos(1/x)當x!=0,且f'(0)=0分開
10/11 01:27, 4F
→
10/11 01:28, 7年前 , 5F
定義 如果一開始沒有定義f(x)=0當x=0就根本沒有f'(0
10/11 01:28, 5F
→
10/11 01:29, 7年前 , 6F
這種情況下就是任f'(0+-)不斷震盪 沒有衝突
10/11 01:29, 6F
→
10/11 01:30, 7年前 , 7F
所以我們不能說f'(0+)和f'(0-)相等 這是一個函數在
10/11 01:30, 7F
→
10/11 01:31, 7年前 , 8F
該處可微分但是微分後不連續的例子
10/11 01:31, 8F
→
10/11 01:33, 7年前 , 9F
由定義做f'(x)=2xsin(1/x)-cos(1/x)當x!=0 =0當x=0
10/11 01:33, 9F
謝謝大大極熱心地回覆了好多ＸＤ 顯然您缺批幣對ㄅ
推
10/11 01:35, 7年前 , 10F
第二個問題f'(0+) = f'(0-) = 0 且 f 在 x = 0 連續
10/11 01:35, 10F
→
10/11 01:36, 7年前 , 11F
這個沒問題阿 直接套入微分定義 f(0)=0 套入定義做
10/11 01:36, 11F
→
10/11 01:36, 7年前 , 12F
f'(0+) = 0 f'(0-) = 0 極限左 = 右 微分存在阿
10/11 01:36, 12F
→
10/11 01:40, 7年前 , 13F
f在x=a連續且f'(a+)與f'(a-)存在且相等<=>微分存在
10/11 01:40, 13F
→
10/11 01:43, 7年前 , 14F
另外,你覺得x^2 * sin(1/x)在x=0處連續嗎?不對吧 這
10/11 01:43, 14F
→
10/11 01:44, 7年前 , 15F
可能就是你的徵結所在 所以題目才要定義f(x)=0當x=0
10/11 01:44, 15F
→
10/11 01:47, 7年前 , 16F
怕第一題回答被誤解f'(x)分開成x!=0和x=0不是人工定
10/11 01:47, 16F
→
10/11 01:48, 7年前 , 17F
義,是直接由題目人工定義的函數導出來的
10/11 01:48, 17F
→
10/11 01:51, 7年前 , 18F
我更正一下 提目定義的x^2 * sin(1/x)在x=0處連續
10/11 01:51, 18F
→
10/11 01:52, 7年前 , 19F
因為加了f(x)=0當x=0 如果沒有題目人工放進f(0)=0
10/11 01:52, 19F
→
10/11 01:52, 7年前 , 20F
純粹x^2 sin(1/x)在x=0是不連續的
10/11 01:52, 20F
如果確定靠定義可以證明 f在x=a連續且f'(a+)與f'(a-)存在且相等==>微分存在， 我會試試～　掰惹位反向未必成立，不過如果f'(a+)與f'(a-)都不存在可能就又可以惹。
推
10/11 02:14, 7年前 , 21F
第一題直觀的解釋 f(x)是奇函數 f'(|a|)=f'(-|a|)
10/11 02:14, 21F
→
10/11 02:16, 7年前 , 22F
本來在x=0的兩旁一直震盪，現在因題目人工強制f(0)=
10/11 02:16, 22F
→
10/11 02:18, 7年前 , 23F
0把震盪強壓成連續函數 所以最後震盪效果平均掉
10/11 02:18, 23F
再次感謝ＸＤ
→
10/11 02:18, 7年前 , 24F
10/11 02:18, 24F
這篇寫得不錯～
→
10/11 02:20, 7年前 , 25F
使題目的函數為連續 也就是震盪被壓制水平掉 所以在
10/11 02:20, 25F
→
10/11 02:22, 7年前 , 26F
f'(0)=0 但是只要不是x=0 就算在x=0附近 還是有震盪
10/11 02:22, 26F
→
10/11 02:23, 7年前 , 27F
震盪在x=0處被人工定義的f(0)=0所水平掉 使f'(0)=0
10/11 02:23, 27F
→
10/11 02:23, 7年前 , 28F
但是人工定義f(0)=0的部份並不會影響到x!=0的函數性
10/11 02:23, 28F
→
10/11 02:24, 7年前 , 29F
質 大概就是這樣
10/11 02:24, 29F
謝謝大大耐心補充
→
10/11 02:25, 7年前 , 30F
抱歉，我以為那邊你剛好講完，斷到了
10/11 02:25, 30F
推
10/11 02:28, 7年前 , 31F
沒關係 甭介意
10/11 02:28, 31F
推
10/11 09:07, 7年前 , 32F
令g=f'，簡單來說就是g在0不連續，所以g(0+)!=g(0)
10/11 09:07, 32F
謝謝大大提到微分連續的觀念～ 對惹批幣我統一星期六再來統計，基本上有回有批，不用拘泥於前三名 ------------------------------------------------------------------------------- 作業已批改完畢，感謝各路好手挺身相助，這邊公布一下批幣分配： yyc2008: 500P Ricestone: 250P sunev: 50P ※ 編輯: alan23273850 (140.112.77.165), 10/12/2018 20:36:11
推
10/12 21:42, 7年前 , 33F
可微就一定連續
10/12 21:42, 33F
→
10/12 21:44, 7年前 , 34F
有個函數處處連續但不可微
10/12 21:44, 34F
‣ 更多 alan23273850 的文章
文章代碼(AID): #1RlYTa61 (Math)
‣ 更多 alan23273850 的文章
文章代碼(AID): #1RlYTa61 (Math)