Re: [微積] 一些關於端點微分判斷的正確觀念

看板Math作者 (312)時間7年前 (2018/10/11 09:41), 7年前編輯推噓4(4推 0噓 8→)
留言12則, 3人參與, 7年前最新討論串2/2 (看更多)
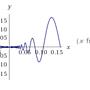
※ 引述《alan23273850 (God of Computer Science)》之銘言： : 各位板友好，洨弟好久沒在板上發文ㄌ，是說洨弟這學期續接了微積分助教， : 為了生活費接下批改作業的重責大任，遇到了一些問題，主要關於端點微分判斷。 : 當然直接套定義可以很簡單算，可是初學者會用一些旁門左道作答。 : 先拿一個題目當開場白： : 給定 f(x) = x^2 * sin(1/x) if x =\= 0, = 0 if x = 0， : https://imgur.com/8vkIXJD
: 請問 f'(0) 存不存在？ : 這題答案是存在的，當然套定義可以簡單看出，因為右導左導都是 0。 : 可是如果對 x^2 * sin(1/x) 作 chain rule 會發現 f'(0+) 和 f'(0-) 都會震盪。 : 這很不直覺，明明不管多靠近都會震盪，最後微分卻會變成 0。 就是因為不直覺才能顯現出這種例子的價值 (這樣答應該是撈不到p幣 所以等等回答第二題) : 不知道針對這個問題是不是有直觀解釋？這是我第一個問題。 : 接下來是問 f(x) = x * |x| 在 x = 0 可不可以微分？ : 答案是可以，卻有人用 f'(0+) = f'(0-) = 0 且 f 在 x = 0 連續來解釋。 : 不知道這樣解釋可ㄅ可以？這是我第二個問題。 這次學妹(?)還真的說對了 以下證明... 若函數 f: R→R 在 (a-ε,a) 以及 (a,a+ε) 可微 且在 [a-ε,a+ε] 連續， for some ε>0 且 f'(a-)、f'(a+)都存在且相等 則 f'(a) 存在，且 f'(a)=f'(a-)=f'(a+) pf: 因 f 在 (a-ε,a) 可微，且在 [a-ε,a] 連續 by MVT 存在 α \in (a-ε,a) such that f(a)-f(a-ε) f'(α)= ------------ (*) ε by MVT again 存在 β\in (a,a+ε) such that f(a+ε)-f(a) f'(β)= ------------ (**) ε 第*式讓 ε→0+，則 α→a- 因f'(a-)存在，所以 f'(a-)=f'-(a) 第**式讓 ε→0+，則 β→a+ 因f'(a+)存在，所以 f'(a+)=f'+(a) 又 f'(a-)=f'(a+) ，因此 f'-(a)=f'+(a) 因此 f'-(a)=f'+(a)=f'(a) -- ※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 218.164.188.241 ※ 文章網址: https://www.ptt.cc/bbs/Math/M.1539222101.A.C9F.html ※ 編輯: ERT312 (218.164.188.241), 10/11/2018 09:45:25 ※ 編輯: ERT312 (218.164.188.241), 10/11/2018 09:46:41
推
10/12 20:36, 7年前 , 1F
感謝大大詳盡的回覆，這個證明有touch到我，我有把
10/12 20:36, 1F
→
10/12 20:37, 7年前 , 2F
它寫進公開在課堂上的詳解了
10/12 20:37, 2F
→
10/12 20:37, 7年前 , 3F
因為這個答案遠超過我的期望，我願意奉送 500P
10/12 20:37, 3F
推
10/14 20:31, 7年前 , 4F
lim_{β→a+} f'(β)=f'(a+)這邊好像不夠充分。
10/14 20:31, 4F
→
10/14 20:32, 7年前 , 5F
因為極限需要a右邊所有的β，可是我們的β都是用ε
10/14 20:32, 5F
→
10/14 20:33, 7年前 , 6F
選出來的，很可能沒有涵蓋到所有該涵蓋到的數字。
10/14 20:33, 6F
→
10/14 21:23, 7年前 , 7F
f'(a+)存在是已給的條件，β不用涵蓋整個區間
10/14 21:23, 7F
→
10/14 22:55, 7年前 , 8F
有個定理是這樣:若lim_{x→a} f(x)=α，則對所有收
10/14 22:55, 8F
→
10/14 22:56, 7年前 , 9F
歛到a的數列 a_n→a，且a_i≠a，有f(a_n)→α as
10/14 22:56, 9F
→
10/14 22:57, 7年前 , 10F
n→∞
10/14 22:57, 10F
推
10/15 02:10, 7年前 , 11F
lim_{β→a+}f'(β)=lim_{ε→0+}[f(a+ε)-f(a)]/ε
10/15 02:10, 11F
推
10/15 02:18, 7年前 , 12F
啊，對，我把符號弄混了。先存在的是LHS。
10/15 02:18, 12F
‣ 更多 ERT312 的文章
文章代碼(AID): #1RlgfLoV (Math)
‣ 更多 ERT312 的文章
文章代碼(AID): #1RlgfLoV (Math)