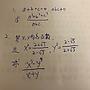Re: [代數] 高中

: 請神人求解:)
記得以前高一常常遇到這種題目,其實我都是利用絕對值的定義去畫線段圖解,
大部分的同學或老師都只教分段討論暴力拆開解方程式的方法,這樣做就浪費這些題目了
雖然線段圖也要分段討論,不過在求解上因為更直觀,所以更理解基本觀念也不太會算錯
那絕對值的定義是什麼呢?「 | a - b | = 數線上 a 和 b 的距離」
你沒看錯!因為很重要,所以這邊強調三次:
| a - b | = 數線上 a 和 b 的距離
| a - b | = 數線上 a 和 b 的距離
| a - b | = 數線上 a 和 b 的距離
有了這個觀念之後,便能將原式進行拆解,|x-7| + |2x+6| = |x+13| 其實就是
|x-(7)| + 2 * |x-(-3)| = |x-(-13)| 這句話意思是要找到一個數字 x,
它 和7的距離 加上 和-3的距離兩倍 等於 到-13的距離。然後一樣要分四個 case:
(Case 1: x > 7)
https://i.imgur.com/Q6aE0Ee.jpg

想讓橘色距離總和等於藍色線段,可以發現 7 左側的兩條橘線剛好等於左側的藍線,剛好
抵銷,那麼剩下 7 右邊的三條橘線要等於一條藍線,想也知道不可能,於是無解。
(Case 2: -3 <= x <= 7)
https://i.imgur.com/FIkdmml.jpg

一樣,我們發現 -3 左邊的藍線剛好跟 -3~7 這段的兩條橘線可互相抵銷,剩下 -3~x 的
一條橘線與一條藍線,他們當然會相等,於是 [-3,7] 這整段都是解。
(Case 3: -13 < x < -3)
https://i.imgur.com/yDJgMOK.jpg

這很明顯無解,因為藍色線段 <= 10,而 x~7 的橘線就超過 10 了。
(Case 4: x <= -13)
https://i.imgur.com/sXvIVjm.jpg

這個也是,每一條橘線都比那條藍線長,更遑論要抵銷。
四種情況都討論完,答案就呼之欲出囉,就是 [-3,7]。
公式化討論拆解法也是一種作法,只是這樣便稍稍缺少了一點數學的樂趣,
根據我的經驗,只要絕對值前面的係數不要太誇張 (5以上),這個方法通常都會比較
直觀且好懂,供您參考。當然也有線段圖法很難看出來的題目,不過真的很少。
--
推
08/19 18:04,
08/19 18:04
推
08/19 18:07,
08/19 18:07
→
08/19 18:08,
08/19 18:08
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 123.193.38.80
※ 文章網址: https://www.ptt.cc/bbs/Math/M.1506188663.A.8BF.html
推
09/24 03:39, , 1F
09/24 03:39, 1F
→
09/24 03:40, , 2F
09/24 03:40, 2F
→
09/24 13:40, , 3F
09/24 13:40, 3F
→
09/24 13:41, , 4F
09/24 13:41, 4F
→
09/24 13:42, , 5F
09/24 13:42, 5F
→
09/24 13:42, , 6F
09/24 13:42, 6F

討論串 (同標題文章)