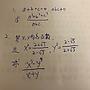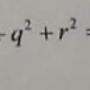Re: [代數] 高中

: 請神人求解,謝謝:)
[x^2 - 4xy + 4y^2] + 2y^2 - 2x - 20y = 29
=> [x - 2y]^2 - 2x + 2y^2 - 20y = 29
=> [x - 2y - 1]^2 - 24y + 2y^2 = 30
=> [x - 2y - 1]^2 + 2[y - 6]^2 = 102
限制x, y均為正整數
(y - 6)^2 <= 51
=> 0 <= y <= 13
y = 13:
x - 27 = +-2
=> x = 29, 25
y = 5:
x - 11 = +-10
=> x = 21, 1
y = 7:
=> x - 15 = +-10
=> x = 25, 5
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 111.243.55.151
※ 文章網址: https://www.ptt.cc/bbs/Math/M.1506089799.A.D96.html
推
09/23 18:31, , 1F
09/23 18:31, 1F
討論串 (同標題文章)