Re: [幾何] 三等分角

看板Math作者Vulpix (Sebastian)時間9年前 (2016/09/23 02:57)推噓2(2推 0噓 11→)

留言13則, 2人參與討論串3/4 (看更多)

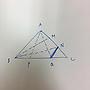
推完漂亮的作法，來貢獻一個暴力的作法首先是這類題目實在太常見了每次看到都在想說又要找一個巧妙的輔助線了或者沒找到的話也是三角函數恆等式的迴圈那乾脆先暴力找個公式放著吧已知△ABC、邊AC上一點N、邊BC上一點Q 並令∠BAC = α、∠ABC = β、∠BAQ = γ、∠ABN = δ WLOG 假設邊AB長1 則由正弦定理可得線段AN = sinδ / sin(α+δ) 線段AQ = sinβ / sin(β+γ) 建立複數坐標，使 A = 0、B = 1、C 位於上半平面則 N = sinδ / sin(α+δ) * exp(iα) Q = sinβ / sin(β+γ) * exp(iγ) 計算 Q-N 的幅角正切值，得 (cotα+cotδ-cotβ-cotγ)/(cotγcotδ-cotαcotβ) 故 ∠BNQ = δ+arctan[(cotα+cotδ-cotβ-cotγ)/(cotγcotδ-cotαcotβ)] 只是這個公式也沒有太好用，有點遺憾 -- ※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 163.13.112.58 ※ 文章網址: https://www.ptt.cc/bbs/Math/M.1474570654.A.CFE.html

推

Desperato

09/23 08:18, , 1^F

09/23 08:18, 1^F

→

Desperato

09/23 08:18, , 2^F

09/23 08:18, 2^F

→

linkismet

09/23 11:25, , 3^F

09/23 11:25, 3^F