Re: [中學] 求梯形面積

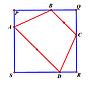
: 如圖
: ABCD為等腰梯形
: 以AD和BC為斜邊作等腰直角三角形ASD&QBC
: 延QB,QC,SA,SD交於P,R
: 已知AS+BQ=10,PQRS周長=50
: 請求出ABCD面積
: P.S.這是自己想出的題
因為三角形ASD與三角形BCQ為等腰直角三角形
=>上底+下底=線段BC+線段AD=線段BQ√2+線段AS√2=(線段BQ+線段AS)√2=10√2
因為三角形ASD與三角形BCQ為等腰直角三角形、且ABCD為等腰梯形
所以角QBC=角QCB=角SAD=角SDA=45度、角CBA=角BCD、角BAD=角CDA
=>角PBA=角RCD、角CDR=角BAP 且線段AB=線段CD
=>三角形BAP與三角形CDR ASA全等
因為 線段PB=線段CR、線段BQ=線段CQ,
且線段PB與線段BQ、線段QC與線段CR分別在同一直線上,
且角PQR、角PSR皆為直角
=>四邊形PQRS為正方形
令線段BC中點為M、線段AD中點為N
高=線段QS-線段QM-線段SN
因為PQRS為正方形,且周長為50
=>正方形PQRS邊長為50/4
=>線段QS為25√2/2
因為三角形ASD與三角形BCQ為等腰直角三角形,且M、N分別為斜邊中點
所以線段QM平分角BQC並垂直於線段BC、線段SN平分角ASD並垂直線段AD,
且三角形ASN與三角形BQM為等腰直角三角形
=>線段QM+線段SN=線段BQ/√2+線段AS/√2=(線段BQ+線段AS)/√2=5√2
高=線段QS-(線段QM+線段SN)=25√2/2-5√2=15√2/2
梯形ABCD面積=(上底+下底)*高/2
=>10√2*15√2/2/2=75
------------以上是經原討論串留言提醒後想出來的---------------------
原本以為證明PQRS為正方形後QMNS自然會在同一直線上
但左思右想後發現PQRS是否為正方形 跟那四點是否在同一直線上很像沒有關係
所以想借串問一下,要怎麼證明他們在同一直線上
目前想法是很像可以利用相似三角形,沿著直線PQ與直線SQ做縮放
可是不知道要怎麼得到他們在同一直線的結論
或是令直線QS在線段BC的交點為M'、直線在線段AD的焦點為N',
只要能證明M'=M、N'=N,應該就可以說明他們在同一直線上
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 1.172.116.46
※ 文章網址: https://www.ptt.cc/bbs/Math/M.1465200777.A.303.html
※ 編輯: carzyallen (1.172.116.46), 06/06/2016 16:15:18
推
06/06 16:18, , 1F
06/06 16:18, 1F
→
06/06 16:18, , 2F
06/06 16:18, 2F
→
06/06 16:18, , 3F
06/06 16:18, 3F
→
06/06 16:24, , 4F
06/06 16:24, 4F
推
06/06 16:27, , 5F
06/06 16:27, 5F
假如要證明的話要怎麼證明直線QS為本圖中的對稱軸?
※ 編輯: carzyallen (1.172.116.46), 06/06/2016 17:15:46
推
06/06 20:27, , 6F
06/06 20:27, 6F
推
06/06 21:33, , 7F
06/06 21:33, 7F
→
06/06 21:34, , 8F
06/06 21:34, 8F
推
06/06 21:37, , 9F
06/06 21:37, 9F
討論串 (同標題文章)