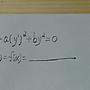Re: [微積] 微分方程
※ 引述《supercake (求知若飢 虛心若愚)》之銘言:
: 題目是
: A'(t)=A(t)^2+A(t)-1,A(0)=0
: 希望版上的大大們可以解惑 謝謝
很久沒碰了 而且答案丟 WolframAlpha 好像頗醜
Riccati eq 就是 y' = y 的二次式 (ex. ay^2+by+c )
-u'(x)
最單純的做法就是 假設 y = ------- 再帶回原式 可以得到 u 的 2nd ODE
a u(x)
-u' -u'u + (u')^2
所以 假設 A(t) = ----- (因為a=1), 則 A'(t) = ------------- 帶回原式
u u^2
-u'u+(u')^2 (u')^2 -u'
=> ------------ = ------- + --- - 1
u^2 u^2 u
整理可得
=> u"-u'-u = 0 ( u 的 2nd ODE)
1+√5 1-√5
(-----)t (------)t
=> u = c1 e 2 + c2 e 2
再將 u'求出 帶回 A(t) = -u'/u 及 A(0) = 0 應該可以得到 c1= (...)c2
整理一下應該就可以得到答案
但是真的有點醜 就有點懶得整理了XDDD
(√5)x
(√5 - 1)(e -1 )
wolfram 的答案是 A(t) = ---------------------
(√5)x
(√5 - 3)e -2
有錯幫糾正阿
--
推
10/26 23:03,
10/26 23:03
推
10/26 23:04,
10/26 23:04
推
10/26 23:04,
10/26 23:04
→
10/26 23:04,
10/26 23:04
→
10/26 23:04,
10/26 23:04
→
10/26 23:04,
10/26 23:04
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 220.137.47.168
※ 文章網址: https://www.ptt.cc/bbs/Math/M.1448790937.A.186.html
推
11/29 18:20, , 1F
11/29 18:20, 1F
→
11/29 18:21, , 2F
11/29 18:21, 2F
討論串 (同標題文章)