Re: [幾何] 一題幾何證明
推
11/19 04:13,
11/19 04:13

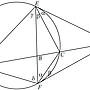
AC:CB = △ACE:△BCE = EC*AE*sinα/2 :EC*EB*sinβ/2 = AEsinα:BEsinβ
同理
AD:DB = △ADE:△BDE = AEsin(α+β+γ):BEsinγ = AEsinδ:BEsinγ
=> AC*DB : CB*AD = sinαsinγ:sinβsinδ --- (1)
====================================================
AC:CB = △ACF:△BCF = AFsinβ:BFsinα
AD:DB = △ADF:△BDF = AFsin(α+β+δ):BFsinδ = AFsinγ:BFsinδ
=> AC*DB : CB*AD = sinβsinδ:sinαsinγ --- (2)
由(1)(2)知 AC*DB : BC*AD = 1 ,所以 AC*DB = BC*AD
這調和性質競賽常出現,通常可直接使用
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 122.121.180.137
※ 文章網址: https://www.ptt.cc/bbs/Math/M.1447924786.A.2F7.html
※ 編輯: FAlin (122.121.180.137), 11/19/2015 17:19:53
推
11/19 17:26, , 1F
11/19 17:26, 1F
推
11/19 22:49, , 2F
11/19 22:49, 2F
討論串 (同標題文章)