看板
[ Math ]
討論串[幾何] 一題幾何證明
共 9 篇文章
內容預覽:
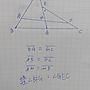
參考. 陳一理. 所編著的"平向". 可知. -> -> ->. MG=(1/2)(AB+DC). 並假設. 角BFG=alpha,角GEC=beta. -> -> -> -> -> -> ->. 則AB dot MG=(1/2)(|AB|^2 dot AB dot DC)=DC dot MG.因此
(還有25個字)
內容預覽:
分別. 從E,F兩點. 至兩邊AB&CD作平行線到BC. 可交於一點P. 於是乎. PEF為一"等腰三角". 最後. 可證明. 角BME=角PEF=角EFP=角CNF (同位角相等). p.s.http://gogeometry.com/NewtonTheorem.htm. 亦可參考. 九章出版"初
(還有21個字)
內容預覽:
另一種證法。. AD取中點G,GE與GF連線。. 因 三角形DAC與三角形GAF SAS相似,. 故 GF平行DC 且 2*GF=DC。. 因 三角形ADB與三角形GDE SAS相似,. 故 GE平行AB 且 2*GE=AB。. 因 GF=1/2*DC=1/2*AB=GE,. 故 三角形GEF為等腰
(還有121個字)
內容預覽:
E與F兩點之座標為:. F=(A+C)/2. E=(B+D)/2. 向量 [FE﹥= E-F. = 1/2*[(B-A)+(D-C)] = 1/2*{ [AB﹥+[CD﹥}. 平移向量 [AB﹥與 [CD﹥,使B點與C點重疊,形成三角形A'B'D'。. 因 [AB﹥+ [CD﹥= 2[FE﹥,[FE
(還有130個字)