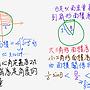
Re: [微積] 如何證明lim sinx/x=1如果面積概念未

看板Math作者JohnMash (Paul)時間10年前 (2015/03/12 22:18)推噓2(2推 0噓 7→)

留言9則, 5人參與討論串2/2 (看更多)

※ 引述《JohnMash (Paul)》之銘言： : ※ 引述《sightseer ()》之銘言： : : 常見的證明lim sinx/x=1 as x approaches 0的方法如下(夾擠定理) : : http://tinyurl.com/kgkuehy : : 其中用到扇形OKA的面積=1/2*R^2*x : : 但是這已經先假設我們已知如何定義並計算扇形面積了 : : 所以如果"面積"概念尚未定義的情況下 : : lim sinx/x=1如何證明? : 我們直接想從圓的弧長要得到sin的微分性質是非常困難的 : 因為弧是曲線要嚴格地證明曲線長度是否存在非常費勁 : 另一方面我們從面積出發卻很容易嚴格地證明圓面積存在(有界連續函數的定積分) : 我們把單位圓的面積記作 A 在數值上可以實際去計算大約是3.14159... : 圓的圓心角是四個直角 : 我們用角度量來記是360 : 現在我刻意避免使用徑度量來記角度因為徑度量牽涉到圓周長我們尚未能嚴格證明它存 : 在 : 於是我們採用一種新的度量記法叫做角的面度量 : 我們把圓的圓心角記作2A : 現在我們將三角函數中的角度一律以面度量表示 : 則很容易從面積的關係得到 : lim sin θ / θ = 1 : 注意上式的 θ 是以面度量表示 : 因此三角函數的微積分大樓從此蓋起 : 然後我們開始嚴格定義弧長 : 於是可證明單位圓的弧長是存在的而且正是2A : 請見附圖 : http://imgur.com/87WRO3s

: 正如用度度量來記角度一樣用角的面度量來記角度 : 所有高中的三角函數公式完全適用 : http://imgur.com/ZuvfxtH

: 如果大家覺得没有問題的話 : 我想把這篇文章整理一下投到數學傳播季刊 : 如果投中的話稿費將拿來請各位討論此系列文的板友吃雞排剛才收到數學傳播的退稿通知主要的理由是“老微積分課本已經有嚴格證明” 我還是把稿子寄給我認識的老師看一下聽聽他們的說法以下是稿子的原文 http://imgur.com/03F2Sxn