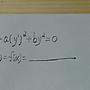Re: [微積] 微分方程
※ 引述《ksxo (aa)》之銘言:
: 看解答看不懂
: 2x - ysin(xy) + {3y^2-xsin(xy)}y' = 0 <= 解微分方程
: 解答: {2x-ysin(xy)} dx + {3y^2 - xsin(xy)}dy = 0
: d{x^2 + ysin(xy) +y^3} = 0
: x^2 + cos(xy) + y^3 = c
: 請問解答第一個式子是怎麼換到第二個式子的? 然後第三個式子是不是少了y?
: 還有第一個式子不能直接兩邊積分嗎?
: 我積分完會得到 x^2 + 2cos(xy) + y^3 = c <= 多了2
不行
第一式子是exact
∫{2x - ysin(xy)}@x = x^2 + cos(xy) + h(y)
∫ {3y^2 - xsin(xy)}@y = y^3 + cos(xy) + r(x)
所以你只寫對一半
x^2 + y^3 + 2cos(xy) + h(y) + r(x) = c'
事實上h(y) = y^3
r(x) = x^2
所以2x^2 + 2y^2 + 2cos(xy) = c'
=> x^2 + 2cos(xy) + y^3 = c
: 和解答不太一樣 謝謝
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 61.228.135.106
※ 文章網址: http://www.ptt.cc/bbs/Math/M.1398855798.A.0F8.html
※ 編輯: Honor1984 (61.228.135.106), 04/30/2014 19:09:03
→
04/30 19:38, , 1F
04/30 19:38, 1F
→
05/01 00:04, , 2F
05/01 00:04, 2F
討論串 (同標題文章)