Re: [中學] 幾何證明題

看板Math作者FAlin (FA（バルシェ應援）)時間12年前 (2013/12/09 23:38)推噓3(3推 0噓 0→)

留言3則, 3人參與討論串2/10 (看更多)

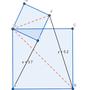
※ 引述《callmedance (中和梁烈唯)》之銘言： : 等腰三角形ABC中，BA=BC ， D在AC邊上，使AD=2DC : 且E在BD上，使角BAE = 角EBC : 證明 : 角CED =1/2 角ABC : 想幾個小時了，還是不會做證明題請高手幫忙謝謝在AE邊上取中點F，S△AFB = S△BFE = (1/2)S△ABE = S△BEC 且BA = BC、∠BAE = ∠CBE，配上面積相等，有△AFB全等於△BEC 可得 BE = AF，因此，BE = AF = FE 最後 ∠ABC = ∠ABF + ∠FBE + ∠DBC = ∠ECB + ∠FBE + ∠DBC = ∠CED + ∠FBE = ∠CED + ∠EBF = ∠CED + ∠CED (∠CED是∠CEB的外角、∠BFE是∠BFA外角) = 2∠CED 得證 -- ※ 發信站: 批踢踢實業坊(ptt.cc) ◆ From: 124.11.128.7

推

callmedance

12/10 13:38, , 1^F

12/10 13:38, 1^F

推

nobrother

12/10 15:45, , 2^F

12/10 15:45, 2^F

推

someone

12/11 18:20, , 3^F

12/11 18:20, 3^F