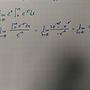[微積] 一題求極限

看板Math作者rebe212296 (綠豆冰)時間13年前 (2012/12/03 00:57)推噓1(1推 0噓 6→)

留言7則, 3人參與討論串1/5 (看更多)

若lim f(x)=lim g(x-a)=0 x→a x→a 則lim f(x+a)g(x)=0 成立嗎? x→0 解: 由極限定義 lim f(x)=lim g(x-a)=0 x→a x→a For all ε>0 there exists a δ>0, 0<|x-a|<δ推得|f(x)|=|g(x-a)|<ε ∵|x-a|≦|x|+|a|, |x-a|<δ ∴|x|<δ-|a|<δ f 代 x+a For all ε>0 there exists a δ>0, 0<|(x+a)-a|<δ推得|f(x+a)|=|g((x+a)-a)|<ε ∴lim f(x+a)=0, lim g(x)=0, x→0 x→0 ∴lim f(x+a)g(x)=0 x→0 這是我想到的不知道有沒有寫錯請版大指教感謝 -- ※ 發信站: 批踢踢實業坊(ptt.cc) ◆ From: 123.193.56.234

→

yhliu

12/03 01:28, , 1^F

12/03 01:28, 1^F

→

yhliu

12/03 01:29, , 2^F

12/03 01:29, 2^F

推

james2009

12/03 03:12, , 3^F

12/03 03:12, 3^F