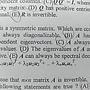[理工] 103中央線代

看板Grad-ProbAsk作者時間7年前 (2019/01/18 19:50), 編輯推噓5(5推 0噓 21→)
留言26則, 3人參與, 7年前最新討論串2/4 (看更多)
https://i.imgur.com/nZ8TIDh.jpg
https://i.imgur.com/Z67L7e8.jpg
這題的答案是abce 我想問的是題目說A是對稱矩陣 然後對稱矩陣可正交對角化 那這題的判斷方法 是要用第二張圖片的Hermitian還是othogonal來判斷 麻煩各位一下 感謝 -- ※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 110.28.137.113 ※ 文章網址: https://www.ptt.cc/bbs/Grad-ProbAsk/M.1547812248.A.826.html
推
01/18 19:54, 7年前 , 1F
用Hermitian判斷
01/18 19:54, 1F
→
01/18 19:55, 7年前 , 2F
因為不一定是othogonal矩陣
01/18 19:55, 2F
→
01/18 20:23, 7年前 , 3F
第二張圖片的正交是指對稱矩陣做完正交對角化後的P嗎，像是A
01/18 20:23, 3F
→
01/18 20:23, 7年前 , 4F
=P^TDP裡的P這樣?
01/18 20:23, 4F
推
01/18 21:49, 7年前 , 5F
第二張圖片的正交矩陣是指符合A*A=I這個定義的矩陣，而你
01/18 21:49, 5F
→
01/18 21:49, 7年前 , 6F
說的P矩陣因為符合那個定義所以是正交矩陣沒錯～
01/18 21:49, 6F
推
01/18 21:51, 7年前 , 7F
你刪掉的那個問題 我那時候回到一半～ Hermitian可以單向
01/18 21:51, 7F
→
01/18 21:51, 7年前 , 8F
推得可對角化 但反推回來不一定 因為不是只有Hermiatian才
01/18 21:51, 8F
→
01/18 21:51, 7年前 , 9F
能正交對角化 所以那應該是一個單向的箭頭
01/18 21:51, 9F
→
01/18 21:55, 7年前 , 10F
A可正交對角化=>A=QΛQ* => A* = (QΛQ*)* = QΛQ* = A
01/18 21:55, 10F
→
01/18 21:59, 7年前 , 11F
啊不對，Λ會變共軛，所以需要實特徵值
01/18 21:59, 11F
→
01/18 22:49, 7年前 , 12F
抱歉我那篇想說問題打的太冗長了 想想還是刪掉好了
01/18 22:49, 12F
→
01/18 22:50, 7年前 , 13F
想問一下，課本上是說A^H=A是hermitian，那A^T=A也可以稱為h
01/18 22:50, 13F
→
01/18 22:50, 7年前 , 14F
ermitian嗎
01/18 22:50, 14F
→
01/18 23:03, 7年前 , 15F
剛剛想到一個問題，正定保證hermitian，hermitian不能保證
01/18 23:03, 15F
→
01/18 23:03, 7年前 , 16F
正定，是不是可以這麼說
01/18 23:03, 16F
推
01/18 23:49, 7年前 , 17F
A^T=A要限制在只佈於實數的時候，稱作實對稱矩陣 可以想成
01/18 23:49, 17F
→
01/18 23:49, 7年前 , 18F
是實數版的Hermitian 然後你下面講的那個是對的沒錯哦～
01/18 23:49, 18F
→
01/19 00:03, 7年前 , 19F
感謝a大熱心講解
01/19 00:03, 19F
推
01/19 01:04, 7年前 , 20F
補充一下～因為我發現好像沒回答到問題XD 如果在複數域 A^T
01/19 01:04, 20F
→
01/19 01:04, 7年前 , 21F
=A不能說是Hermitian，因為他不滿足定義 https://i.imgur.c
01/19 01:04, 21F
→
01/19 01:04, 7年前 , 22F
om/pMV1qO8.jpg
01/19 01:04, 22F
→
01/19 01:04, 7年前 , 23F
01/19 01:04, 23F
→
01/19 01:05, 7年前 , 24F
抱歉第一次po圖片～
01/19 01:05, 24F
→
01/19 03:47, 7年前 , 25F
實矩陣的話在複數域上也是Hermitian，因為對實矩陣來說
01/19 03:47, 25F
→
01/19 03:47, 7年前 , 26F
A^T=A^H
01/19 03:47, 26F
‣ 更多 AAQ8 的文章
文章代碼(AID): #1SGRsOWc (Grad-ProbAsk)
‣ 更多 AAQ8 的文章
文章代碼(AID): #1SGRsOWc (Grad-ProbAsk)