看板 [ Math ]
討論串[中學] 一題幾何題
共 3 篇文章
內容預覽： 開啟 | 關閉 | 只限未讀
首頁
上一頁
1
下一頁
尾頁
#3
Re: [中學] 一題幾何題
推噓4(4推 0噓 6→)留言10則，0人參與, 7年前最新作者Honor1984 (奈何上天造化弄人？)時間7年前 (2018/09/22 17:06), 編輯資訊
0
1
0
內容預覽:
延長AD到A'使AD = DA'. 過E作BC的垂直線並延長交BA'延長線於B'. 因為EB = EB'. => ∠EBB' = ∠EB'B = ∠AA'B = ∠BAD. => (3/2)∠ABC = ∠BAD. 又因為∠ABC + ∠BAD = 90. => ∠BAC = 2∠BAD = 108
#2
Re: [中學] 一題幾何題
推噓0(0推 0噓 0→)留言0則，0人參與, 最新作者wayne2011 (就愛她白內衣色誘)時間7年前 (2018/09/21 11:50), 7年前編輯資訊
0
1
0
內容預覽:
參考. 九章出版. 所編著的"初幾研究" & "中數辭典". 可知GB=4FD,BE=4FDcos(B/2). =2csinB,FD=csin(B/2). CE/EA=CF/FD,a/c=(abcosC/c+a)/[csin(B/2)]. sin(B/2)=bcosC/(c+a). a=2(c+a)
(還有206個字)
#1
[中學] 一題幾何題
推噓5(5推 0噓 4→)留言9則，0人參與, 7年前最新作者FocusE (專注)時間7年前 (2018/09/18 17:04), 7年前編輯資訊
0
1
0
內容預覽:
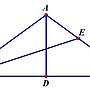
△ABC是等腰三角形，AB=AC，BE是∠ABC的平分線，AD是底邊上的高。. 若BE＝2AD，則∠BAC＝?. https://i.imgur.com/IgKYiOt.png. ----------------------------------------------------------.
(還有110個字)
首頁
上一頁
1
下一頁
尾頁