Re: [中學] 級數問題
※ 引述《knuk (金鋒)》之銘言:
: 大家好,剛被問了一題
: 題目如下
: 從1/2、1/3、...、1/99任意選取奇數個相乘
: 所有這些乘積的總和為S,則最接近S的整數為何?
: 再麻煩各位教學一下,感恩
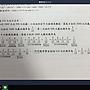
所求S= (1-1/2)*(1-1/3)*...*(1-1/99) 展開之負項和(奇數個乘積)
= [ (1+1/2)*(1+1/3)*...*(1+1/99) - (1-1/2)*(1-1/3)*...*(1-1/99)] / 2
全項和 - (正項和-負項和 ) =2倍負項和
= [ 50 - (1/99) ]/2
= 25 - 1/198
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 36.224.6.118 (臺灣)
※ 文章網址: https://www.ptt.cc/bbs/Math/M.1692692579.A.DBE.html
推
08/22 17:10,
2年前
, 1F
08/22 17:10, 1F
討論串 (同標題文章)