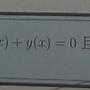Re: [微積] 工數一題

: 這題的入是複數
: 我去網路上都只找得到求通解
: 找不到求yp跟yh的
: 求各位大神開示
y'' + 4y' + 13y = 3exp(-x)
yh : y'' + 4y' + 13y = 0 --> let y = exp(kx), --> k^2 + 4k + 13 = 0
--> (k+2)^2 + 3^2 = 0 --> k = -2±3i
--> yh = exp(-2x)*[Acos(3x) + Bsin(3x)]
yp : y'' + 4y' + 13y = 3exp(-x) --> let y = Cexp(-x)
--> yp = C - 4C + 13C = 3 --> C = 3/10
y = yh + yp = exp(-2x)*[Acos(3x) + Bsin(3x)] + 0.3exp(-x)
--
!!!!!!!!!!!!!簽名檔破2400000點擊率啦!!!!!!!!!!!!!!!
Fw: [問卦] 電影:決勝21點的機率問題 https://goo.gl/2BpbB7 #1MfN3FgZ (joke)
→
07/22 16:41,
07/22 16:41
chx64註冊tisen這帳號是想幹嘛啊?哈哈哈
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 39.9.30.52 (臺灣)
※ 文章網址: https://www.ptt.cc/bbs/Math/M.1573363732.A.75D.html
→
11/10 14:40,
6年前
, 1F
11/10 14:40, 1F
討論串 (同標題文章)