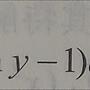[微積] 一題微分方程請教

看板Math作者 (leeleo)時間6年前 (2019/08/12 19:35), 編輯推噓3(3推 0噓 9→)
留言12則, 4人參與, 6年前最新討論串1/2 (看更多)
題目如下，自己試過很多做法了，還是找不出，想請教各位一下，謝謝。 https://i.imgur.com/yzSygtk.jpg
-- ※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 124.9.129.79 (臺灣) ※ 文章網址: https://www.ptt.cc/bbs/Math/M.1565609710.A.4DE.html
→
08/12 19:52, 6年前 , 1F
後面應該是 dy ... -lny - 1)dy = 0
08/12 19:52, 1F
推
08/12 20:15, 6年前 , 2F
題目錯了吧
08/12 20:15, 2F
→
08/12 20:36, 6年前 , 3F
啊啊..抱歉忘了說了，應該是dy才是，不過就算是dy
08/12 20:36, 3F
→
08/12 20:36, 6年前 , 4F
還是不知道該如何算...
08/12 20:36, 4F
推
08/12 20:48, 6年前 , 5F
y/xdx+(lnx-lny-1)dy=0 檢查非正則，考慮積分因子
08/12 20:48, 5F
→
08/12 20:50, 6年前 , 6F
p(x，y)dx+q(x，y)dy=0 r=[patrtialp/partialy-
08/12 20:50, 6F
→
08/12 20:51, 6年前 , 7F
partialq/partialx)/q，r=-1/x M=e^積分rdx
08/12 20:51, 7F
→
08/12 20:54, 6年前 , 8F
M=1/x乘入方程，方程變為y/xdx+(lnx-lny-1)dy=0
08/12 20:54, 8F
→
08/12 20:56, 6年前 , 9F
patialF/partialx=y/x partialF/partialy=lnx-lny-
08/12 20:56, 9F
推
08/12 20:59, 6年前 , 10F
1 再湊出F=ylnx-ylny+c故F=constant得
08/12 20:59, 10F
→
08/12 21:00, 6年前 , 11F
ylnx-ylny=constant
08/12 21:00, 11F
→
08/12 23:10, 6年前 , 12F
感謝。
08/12 23:10, 12F
‣ 更多 ac01965159 的文章
文章代碼(AID): #1TKKxkJU (Math)
‣ 更多 ac01965159 的文章
文章代碼(AID): #1TKKxkJU (Math)