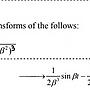Re: [其他] 拉氏逆轉換

看板Math作者 (Bingo)時間6年前 (2019/07/07 20:52), 編輯推噓3(3推 0噓 3→)
留言6則, 2人參與, 6年前最新討論串3/3 (看更多)
※ 引述《Yic0197 (科科科55)》之銘言： : https://imgur.com/c6I8cpP
: 有兩題拉氏逆轉換~ : 目前想到用摺積去做，不過很母湯QQ : 題目應該也不是希望我們用摺積做 : 也有附提示 : 希望有神人幫提點!!! 個人意見：把函數看成三個函數的乘積，再用摺積做兩次！ 用34703的反轉公式要計算兩個極點的3階留數，毎個又要微分兩次，計算未必比較簡單！ ----- Sent from JPTT on my Sony C6902. -- ※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 219.68.168.29 (臺灣) ※ 文章網址: https://www.ptt.cc/bbs/Math/M.1562503951.A.321.html
推
07/07 23:17, 6年前 , 1F
推這篇和上面留數的文。所以已知有部分分式法、摺積
07/07 23:17, 1F
→
07/07 23:17, 6年前 , 2F
法、VULPIX大的構造新變數偏微分、以及留數法。
07/07 23:17, 2F
推
07/07 23:32, 6年前 , 3F
個人認為不同方法表現出不同的結構，可以增加我們對
07/07 23:32, 3F
→
07/07 23:33, 6年前 , 4F
定理的了解。考試再用快的方法就好了。都是很好的方
07/07 23:33, 4F
→
07/07 23:33, 6年前 , 5F
法
07/07 23:33, 5F
推
07/08 12:41, 6年前 , 6F
有給那個hint應該就不會想去用Residue
07/08 12:41, 6F
‣ 更多 bl2086 的文章
文章代碼(AID): #1T8UiFCX (Math)
討論串 (同標題文章)
本文引述了以下文章的的內容：
完整討論串 (本文為第 3 之 3 篇)：
排序： 最新先 | 最舊先 | 留言數
在新視窗開啟完整討論串 (共3篇)
‣ 更多 bl2086 的文章
文章代碼(AID): #1T8UiFCX (Math)