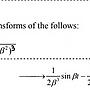Re: [其他] 拉氏逆轉換

: 有兩題拉氏逆轉換~
: 目前想到用摺積去做,不過很母湯QQ
: 題目應該也不是希望我們用摺積做
: 也有附提示
: 希望有神人幫提點!!!
稍微省略一點括弧,因為加進去會有點亂。希望不會讓你誤會分母。
(s^2+β^2)^-2 的逆轉換是 sin(βt)/2β^3 -tcos(βt)/2β^2,
所以 (s^2+β^2)^-2 對β的偏導函數 的逆轉換是
sin(βt)/2β^3 -tcos(βt)/2β^2 對β的偏導函數。
也就是說 -4β(s^2+β^2)^-3 的逆轉換是
((βt)^2 -3)sin(βt)/2β^4 +3tcos(βt)/2β^3。
所以 (s^2+β^2)^-3 的逆轉換是 (3 -(βt)^2)sin(βt)/8β^5 -3tcos(βt)/8β^4。
至於 s^2(s^2+β^2)^-3 = (s^2+β^2)^-2 - β^2(s^2+β^2)^-3 的逆轉換是
sin(βt)/2β^3 -tcos(βt)/2β^2 + ((βt)^2-3)sin(βt)/8β^3 +3tcos(βt)/8β^2
= ((βt)^2 +1)sin(βt)/8β^3 -tcos(βt)/8β^2。
我沒有驗算過,等一下丟鎢α算算看。
果然有錯,少了 t^2。
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 61.230.130.160 (臺灣)
※ 文章網址: https://www.ptt.cc/bbs/Math/M.1561827643.A.A86.html
※ 編輯: Vulpix (61.230.130.160 臺灣), 06/30/2019 01:09:37
推
06/30 01:44,
6年前
, 1F
06/30 01:44, 1F
推
07/01 12:56,
6年前
, 2F
07/01 12:56, 2F
討論串 (同標題文章)