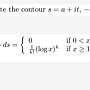Re: [其他] 複變一題

看板Math作者 (奈何上天造化弄人？)時間7年前 (2018/11/04 02:23), 編輯推噓1(1推 0噓 9→)
留言10則, 3人參與, 7年前最新討論串5/5 (看更多)
※ 引述《j123783391 (盧盧)》之銘言： : https://i.imgur.com/OM3cTdj.jpg
: 第二小題 : 完全看不懂 (x - i)/(x^2 + 1) = 1/(x + i) ∞ [1/(2πi)]∫1/[(x + i)(x - z')] dx -∞ = [1/(2πi)]∫f(z)/(z - z')] dz 上半圓 = 1/[z' + i] = f(z') => f(z) = 1/[z + i] -- ※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 111.241.154.29 ※ 文章網址: https://www.ptt.cc/bbs/Math/M.1541269383.A.A10.html
推
11/04 13:37, 7年前 , 1F
謝謝你的回答 可是他的答案是這樣 https://i.imgur.
11/04 13:37, 1F
→
11/04 13:37, 7年前 , 2F
com/15Ar4Mm.jpg
11/04 13:37, 2F
→
11/04 13:38, 7年前 , 3F
11/04 13:38, 3F
→
11/04 13:38, 7年前 , 4F
11/04 13:38, 4F
→
11/04 20:03, 7年前 , 5F
突然不太董原原po你上板問的意義。有人給了你解答，
11/04 20:03, 5F
→
11/04 20:03, 7年前 , 6F
你卻選擇質疑他並相信那本錯誤的書？
11/04 20:03, 6F
→
11/04 20:28, 7年前 , 7F
V大 沒關係啦 其實我當初也有考量到z=i的狀況 只是
11/04 20:28, 7F
→
11/04 20:28, 7年前 , 8F
結果一樣 我就沒有特別多寫了
11/04 20:28, 8F
→
11/04 20:30, 7年前 , 9F
要不是有給hint，不然直接驗證1/(z+i)就了結了。
11/04 20:30, 9F
→
11/04 20:33, 7年前 , 10F
題目可能就是想要讓讀者練習吧?
11/04 20:33, 10F
‣ 更多 Honor1984 的文章
文章代碼(AID): #1RtUU7eG (Math)
討論串 (同標題文章)
本文引述了以下文章的的內容：
完整討論串 (本文為第 5 之 5 篇)：
排序： 最新先 | 最舊先 | 留言數
在新視窗開啟完整討論串 (共5篇)
‣ 更多 Honor1984 的文章
文章代碼(AID): #1RtUU7eG (Math)