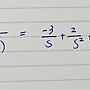Re: [微積] 部份分式問題
最快的作法應該是 Heaviside Method
訣竅是遮蔽想要求解的項次
剩下分式代入令該項次為 0 的值
順帶一提
當有重根的時候
直接使用這個方法只能得到最高重根項次的係數
套用這個概念的話
4 a b c d
---------------- = ----- + --- + ----- + -----
s^2 (s+1)(s+2) s^2 s s+1 s+2
a: 遮掉 s^2 項
左式其他部份的 s 代入 0
4
=> a = ---------- = 2
(0+1)(0+2)
同理
c = 4
d = -1
只剩下 b 不知道的情況下用待定係數只比一個就快多了
[以下為進階部份 看得懂就好 看不懂也無妨]
想知道 b 還有一些取巧作法
等式兩邊同乘以 s
令 s = ∞
4 2 1 2
=> 左式 = ---- = 0 = ---- + b + (1 - ------) * 4 + (1 - ------) * (-1)
∞ ∞ ∞+1 ∞+2
得 0 = b + 4 - 1
b = -3
如果討厭取巧作法想要用 HM 乖乖一步一步做的話就先拆重根項
4 1 4
---------------- = ---[-------------]
s^2 (s+1)(s+2) s s(s+1)(s+2)
1 2 -4 2
= ---(--- + ----- + -----)
s s s+1 s+2
2 -4 2
= ----- + -------- + --------
s^2 s(s+1) s(s+2)
2 -4 4 1 -1
= ----- + ---- + ----- + --- + -----
s^2 s s+1 s s+2
2 -3 4 -1
= ----- + ---- + ----- + -----
s^2 s s+1 s+2
如果連遮蔽法都覺得是取巧作法不想用的話
那就乖乖用待定係數一項一項乘開然後比較係數吧
老天爺最愛努力的人了
※ 引述《johnny00517 (水梨先生)》之銘言:
: https://i.imgur.com/ForzqFz.jpg

: 在解拉氏轉換遇到這個部份分式,
: 不知道要如何處理卡了好久,
: 明明過了這步答案就快出來了,
: 但就是卡在這邊,
: 有哪位大大可以幫我解釋它是怎麼換過去的嗎?
: 感恩不盡
--
そうして、また春になった。
年月は瞬きほど。
目蓋を閉じて、開く。
丘には一面の櫻の花。
懐かしい坂道からは、
あの頃の姿のまま、少年が手を振って── Heaven's Feel《櫻の夢》
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 223.136.79.121
※ 文章網址: https://www.ptt.cc/bbs/Math/M.1539620844.A.61C.html
推
10/16 04:24,
7年前
, 1F
10/16 04:24, 1F
討論串 (同標題文章)