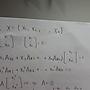Re: [線代] 幾題線代
※ 引述《Aquarkbrain (腦容量只有夸克)》之銘言
: Let R^n be regarded as column vectors.
: 2. Let X be the linear subspace of R^2*3 containing all matrices whose co
lumns
: add to 0 ∈ R^2. Similarly let Y be the subspace of R^2*3 containing all
ma
: trices whose rows add to 0 ∈R^3.
: (a) What is the dimension of X.
: (b) What is the dimension of (X+Y).
(a) A in X, A =
[ a b c ]
[ d e f ]
then X = { A in X | a+b+c = 0, d+e+f = 0 }
Let T: R^2*3 -> R^2, T(A) = (a+b+c, d+e+f)
then T is surjective and kerT = X
by dimension theorem dimX = 4
similarly dimY = 3
(b) consider A in X cap Y
take a, b arbitrary we have A =
[ a b -a-b ]
[ -a -b a+b ]
Now dim(X+Y) = dimX + dimY - dim(X cap Y)
= 4 + 3 - 2 = 5
we can also observe that
[ 0 0 -1 ]
[ 0 0 1 ] in Y but not in X, and
[ 0 0 0 ]
[ 0 0 1 ] not in X+Y
thus dimX < dim(X+Y) < dimR^2*3
but the latter one is not easy to prove though
----
Sent from BePTT
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 49.214.225.10
※ 文章網址: https://www.ptt.cc/bbs/Math/M.1530936370.A.478.html
討論串 (同標題文章)