Re: [線代] 高中圓方程式

看板Math作者aromaQ626 (摳咪霉庇)時間8年前 (2017/11/13 22:26)推噓1(1推 0噓 6→)

留言7則, 3人參與討論串3/3 (看更多)

※ 引述《coco77011 (ooo)》之銘言： : http://i.imgur.com/Ai473tF.jpg

http://i.imgur.com/JIRGzJH.jpg

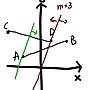
啊我說你要問哪題也沒說 9. (第一張圖) 3x - y + k = 0 => y = 3x + k 這個代表所有斜率為 3 的直線畫出一條 m = 3 的直線並左右調整使他能夠通過AB、CD線段 http://i.imgur.com/DOCU77i.jpg

如圖會發現只有移動到咖啡色與綠色之間的部分能夠符合要求咖啡色線方程式：y = 3x 綠色線方程式：y = 3x + 7 => 0 <= k <= 7 9. (第二張圖) 半徑為 5，且過 P、Q 兩點的圓 => OP = 5 = OQ (O 為圓心) 令O座標為 (x, y) 則 OP = ( (x + 1)^2 + y^2 )^(1/2) = 5 且 OQ = ( (x - 6)^2 + (y + 7)^2 )^(1/2) = 5 解 (x, y) 或是可以畫個圖解 http://i.imgur.com/I9y5Kef.jpg

如圖 M 為 PQ 中點 (5/2, -7/2) 則 OM = ((7sqrt2)^2 + 5^2 )^(1/2) = 1/sqrt2 O = M + (1/2, 1/2) 或 M - (1/2, 1/2) 10. (x - 1)^2 + (y - 4)^2 = 9 過點 (3, -2) 的直線 mx - y - 3m -2 = 0 與 (1, 4) 距離為 3 |m - 4 - 3m - 2| / (m^2 + 1)^(1/2) = 3 (2m + 6)^2 = 9(m^2 + 1) -5m^2 + 24m + 27 = 0 求 m 後代回去直線方程式再分別與圓聯立求A、B兩點再找PAB任兩邊的中垂線求焦點即為PAB外心再算外心到PAB任意頂點即為外接圓半徑打到一半覺得太累了數字又醜就先這樣 --

推

uhmeiouramu

02/02 22:03,

02/02 22:03

→

strike5566

02/02 22:11,

02/02 22:11

推

ccchenny

02/02 22:11,

02/02 22:11