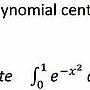Re: [微積] 複習卡關求提點

: 真的想了好久
: 找不到F(X)的微分規律
: 需要提點 謝謝 感激不盡
若 q(x) = p(x)*e^(-x^2)
則 q'(x) = p'(x)*e^(-x^2) + p(x)*(-2x)*e^(-x^2)
= (p'(x) - 2xp(x))e^(-x^2)
所以要求各階微分一次一次代下去即可
p(x) = 1 => p'(x) - 2xp(x) = -2x
p(x) = -2x => p'(x) - 2xp(x) = 4x^2 - 2
p(x) = 4x^2 - 2 => p'(x) - 2xp(x) = -8x^3 + 12x
繼續算下去是 16x^4 - 48x^2 + 12
-32x^5 + 160x^3 - 120
64x^6 - 480x^4 + 720x^2 - 120
所以所求的六階泰勒展開式即為 1 - 2x^2/2! + 12x^4/4! - 120x^6/6!
= 1 - x^2 + x^4/2 - x^6/6
接下來的積分近似就略過了
====
重點是這題只要你求六階近似
那麼既然最多就微六次, 先微再說, 有沒有規律都沒差
又不是要你寫整個級數出來
--
'You've sort of made up for it tonight,' said Harry. 'Getting the
sword. Finishing the Horcrux. Saving my life.'
'That makes me sound a lot cooler then I was,' Ron mumbled.
'Stuff like that always sounds cooler then it really was,' said
Harry. 'I've been trying to tell you that for years.'
-- Harry Potter and the Deathly Hollows, P.308
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 123.195.53.205
※ 文章網址: https://www.ptt.cc/bbs/Math/M.1466541422.A.8A5.html
推
06/22 16:40, , 1F
06/22 16:40, 1F
→
06/22 17:59, , 2F
06/22 17:59, 2F
討論串 (同標題文章)