Re: [中學] 請問一題國二幾何難題

看板Math作者jetzake (加菲貓)時間10年前 (2015/05/16 06:52)推噓0(0推 0噓 16→)

留言16則, 2人參與討論串5/5 (看更多)

※ 引述《jenshi (小旭)》之銘言： : http://www.fotopu.com/fullsize/830512 : CD=6、AD=10、BE=4 : BD是角ADC角平分線 : 求BF？ : 八年級全班沒人會， : 老師只說用九年級的相似很好解， : 但八年級還沒相似， : 大大們有其他解法嗎？謝謝；）如果有給∠C是直角的話這題就很好做.. (當然前兩篇Honor1984兄和XII兄的做法也行只是都需要這個條件...) 我這邊也PO個我的解法吧先上圖... http://i.imgur.com/1gHAMA4.jpg

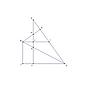
這邊把需要的東西通通標上去 I點是BF延長和AD的交點 J則是B點對CD延長線的垂足首先有了∠ACD是直角這件事的話因為BF和CD都對AC線段垂直可以有∠BDC＝∠BDA＝∠DBF這件事 (前兩者是因為角平分線後面是平行線內錯角相等) 然後 BE=BJ=4 (角平分線任一點對兩邊距離相等或是用全等三角形証出來) 接下來有BJ=CF(=4)=AF → F是AC中點 (AC=8可以推算出來不詳述) 可以知道BF延長出去交AD的I點就是AD中點得到DI=(1/2)AD=5 由∠BDI=∠DBI得知 ⊿BDI為等腰三角形 BI=DI=5 而FI長度又是CD的一半 (FI=3) (*這裡我不確定能不能用中點連線=底邊的一半這個性質不行的話就用AFI這個直角三角形去推算就是) BF=BI-FI=2就這麼推出來了 ===== 雖然看起來有點囉唆但這個方式直接在黑板上畫圖是很自然很流暢的提供給你參考參考... -- ※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 1.164.11.31 ※ 文章網址: https://www.ptt.cc/bbs/Math/M.1431730339.A.12F.html

→

yyc2008

05/16 15:13, , 1^F

05/16 15:13, 1^F

→

yyc2008

05/16 15:15, , 2^F

05/16 15:15, 2^F

→

yyc2008

05/16 15:15, , 3^F

05/16 15:15, 3^F