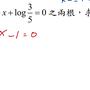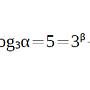Re: [中學] 指對數
※ 引述《booksy (書呆)》之銘言:
: ※ 引述《adamchi (adamchi)》之銘言:
: : 方程式(logx)^2-[logx]-2 = 0 的解 x = _____ ( PS:[ ]是高斯符號 )
: : 答: 100或1/10或10^根號3
: 若logx為整數,則 (logx)^2-logx-2=0 所以logx=2或-1
: x=100或1/10
: 若logx不為整數,則(logx)^2=[logx]+2
: (>0)
: 因為logx-[logx]<1 所以 0<logx<2(應該會有更完備的方法QQ)
: 所以[logx]=1 , (logx)^2=3 , logx=3^(1/2) x=10^(根號3)
利用logx-1<[logx]≦logx
可得logx+1<[logx]+2≦logx+2
故logx+1<(logx)^2≦logx+2
=>(logx)^2-logx-1>0 且 (logx)^2-logx-2≦0
=>"logx>(1+√5)/2 或 logx<(1-√5)/2" 且 "-1≦logx≦2"
得-1≦logx<(1-√5)/2<-0.6 或 1.6<(1+√5)/2<logx≦2
則[logx]=-1,1,2 => (logx)^2=1,3,4 => logx= -1,√3, 2
得x=1/10, 10^√3, 100
: : 設x,y,z皆為實數,且2^x+3^y+5^z=7,2^(x-1)+3^y+5^(z+1)=11,
: : 若a < 2^(x+1)+3^y+5^(z-1) < b ,則數對(a,b)=____
: : 答: (31/5,11)
: : 請問怎麼算得答案,謝謝
: 令A=2^x , B=3^y , C=5^z
: 則A+B+C=7 , 2A+B+5C=11 後式減前式可得 A+4C=4
: 所求=2A+B+1/5C=(2A+B+5C)-24/5C=11-24/5C
: 又 A=2^x=4-4C > 0 得 0 < C=5^z < 1
: 所以所求範圍為 31/5 = 11-24/5*1 < 2A+B+1/5C < 11-24/5*0 = 11
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 210.244.73.99
※ 文章網址: http://www.ptt.cc/bbs/Math/M.1407622063.A.7C3.html
推
08/10 10:55, , 1F
08/10 10:55, 1F
推
08/13 17:29, , 2F
08/13 17:29, 2F
→
08/14 23:39, , 3F
08/14 23:39, 3F
討論串 (同標題文章)