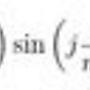Re: [微積] 同學給我的題目(三角函數的Σ)
※ 引述《skbb2553 (HS)》之銘言:
: 標題: [微積] 同學給我的題目
: 時間: Sun Jun 8 00:32:19 2014
:
:
: 證明題 http://i.imgur.com/zoLB1yt.jpg
: (條件:r s=1, 2, 3, ....n)
:
: 想法:積化和差->泰勒展開->Σ對調->整理
:
:
:
: Σ {sin( j (r/n+1) π ) sin ( j (s/n+1) π ) }
修一個打字錯誤,是相乘不是相加。下面就沒錯...
: =Σ {cos( (r-s) (jπ/n+1) )- cos( (r+s) (jπ/n+1) ) }
...但是你這行前面又少了 1/2
: =Σ cos( (r-s) (jπ/(n+1)) )
: -Σ cos( (r+s) (jπ/(n+1)) )
:
(以下刪)
這個公式是Fourier basis的內積,非常重要一定要學起來。
所以重點是要做
n
Σ cos[ (kπ/n+1) j ]
j = 1
這個和。一開始把 k 取為整數就好。
1. 因為 cos 是偶函數,所以可以 k --> -k,只考慮 k >= 0。
2. 若 k > 2(n+1),多出來的部分只會給你一堆 2π,不重要。
所以只要看
k' = k mod 2(n+1)
就好了。
3. 使用 cos(x) = - cos(π- x) :
若 k' != 0,則
cos[(k'π/n+1) * 1] = -cos[(k'π/n+1) * n]
cos[(k'π/n+1) * 2] = -cos[(k'π/n+1) * (n-1) ]
...
n 是偶數的話,整個級數就直接自己相消掉了。若 n 是奇數,還會留下正中間
j = (n+1)/2
這一項。但是把這一項代進去還是 cos( k'π/ 2 ) = 0。
4. 若 k' = 0 每一項都是 1。
5. 其餘請自己補上。
--
若不限 r, s 的範圍,只要求它們是整數,更一般的結果是
(r + s) mod 2(n+1) = 0
時級數和不是零。
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 123.110.172.25
※ 文章網址: http://www.ptt.cc/bbs/Math/M.1402240275.A.309.html
※ 編輯: wohtp (123.110.172.25), 06/08/2014 23:13:59
※ 編輯: wohtp (123.110.172.25), 06/08/2014 23:14:29
推
06/09 00:26, , 1F
06/09 00:26, 1F
→
06/09 00:27, , 2F
06/09 00:27, 2F
→
06/09 00:27, , 3F
06/09 00:27, 3F
推
06/09 01:07, , 4F
06/09 01:07, 4F
討論串 (同標題文章)
完整討論串 (本文為第 2 之 2 篇):