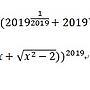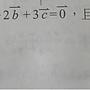Re: [中學] 一題高中數學

看板Math作者 (我有問題)時間12年前 (2013/08/08 09:00), 編輯推噓0(0推 0噓 5→)
留言5則, 3人參與, 最新討論串15/36 (看更多)
※ 引述《Intercome (今天的我小帥)》之銘言： : ※ 引述《wanling0419 (Wanling)》之銘言： : : 若1/1 + 1/1+(1+2) + 1/1+(1+2)+(1+2+3) + 1/1+(1+2)+(1+2+3)+(1+2+3+4) +...+ : : 　1/1+(1+2)+(1+2+3)+...+(1+2+3+4+5+...+18+19+20) = ? : : 題目如上，感謝。 : n : __ : 分母為 \ k(k+1) 1 : ㄥ -------- = ---n(n+1)(n+2) : k=1 2 6 請問1+(1+2)+(1+2+3)+(1+2+3+4)+.....+(1+2+3+....n) 怎麼看出規律是 k(k+1) ------- 2 本來想法是1+3+6+10+......每個都差2.3.4.5........ -- ※ 發信站: 批踢踢實業坊(ptt.cc) ◆ From: 112.105.192.50
→
08/08 10:58, , 1F
不就是連續整數和嗎?
08/08 10:58, 1F
→
08/08 10:58, , 2F
1+2+3+...+n=(1+n)*n/2
08/08 10:58, 2F
→
08/08 11:00, , 3F
欸...k(k+1)/2分別是1, (1+2), (1+2+3), ...
08/08 11:00, 3F
→
08/08 11:01, , 4F
所以最後還要再加在一起才是1+(1+2)+(1+2+3)+...
08/08 11:01, 4F
→
08/08 11:34, , 5F
哦 原來是每個整數和相加 取sigma
08/08 11:34, 5F
‣ 更多 g418 的文章
文章代碼(AID): #1I0ksdMI (Math)
討論串 (同標題文章)
本文引述了以下文章的的內容：
完整討論串 (本文為第 15 之 36 篇)：
排序： 最新先 | 最舊先 | 留言數
在新視窗開啟完整討論串 (共36篇)
‣ 更多 g418 的文章
文章代碼(AID): #1I0ksdMI (Math)