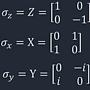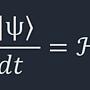[瓦特] 物理研討會-Quantum Computing:0000已回收

看板Marginalman作者 (菁櫻巫女)時間2年前 (2023/02/02 03:08), 編輯推噓6(7推 1噓 7→)
留言15則, 11人參與, 2年前最新討論串4/6 (看更多)
現在來講接下來的量子公設:00 公設2: 任何可以被測量的物理量，都可以由狀態空間裡的運算子H來描述 而這個運算子必定會是厄米特運算子(Hermitian operator) 對於封閉狀態空間，也就是跟環境沒有任何互動的狀態空間而言 量子態隨著時間的演變可以寫作 https://imgur.com/N0RqBz5.jpg
右邊那個H就是哈密頓量 (Hamiltonian) 描述系統的總能量 相對的 動量 位置 這些物理量也都可以寫成一個運算子 只是在這裡還不太會用到 在這裡比較重要的點是 厄米特運算子遵從幾個點 1. 厄米特運算子的轉置再共軛會等於自己 2. 厄米特運算子的本徵值(Eigenvalue)一定為實數 前面提到 如果在 封閉系統中 還會多出一條重要的規則 3. 這個隨時間推演的運算子必定會是么正矩陣(unitary matrix) https://imgur.com/3R5ocj6.jpg
這條專屬於封閉狀態空間的規則實際上的物理意義是 時間推演不會影響到量子態的量 https://imgur.com/NSRxTDW.jpg
中間那項U+ U之所以可以寫成1 (其實應該是I 單位矩陣) 是因為么正矩陣的特性 然後<φ|I|φ> 就會因為公設1變成1 -- https://imgur.com/TtCJPhE.gif
-- ※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 128.210.106.60 (美國) ※ 文章網址: https://www.ptt.cc/bbs/Marginalman/M.1675278515.A.D7E.html
推
02/02 03:10, 2年前 , 1F
大師:000
02/02 03:10, 1F
→
02/02 03:10, 2年前 , 2F
姆咪還是煮牛肉麵
02/02 03:10, 2F
推
02/02 03:11, 2年前 , 3F
大一菜逼看不懂捏:0000
02/02 03:11, 3F
→
02/02 03:13, 2年前 , 4F
:ooooooooooooooo:
02/02 03:13, 4F
推
02/02 03:14, 2年前 , 5F
大師 :00000
02/02 03:14, 5F
推
02/02 03:15, 2年前 , 6F
跟我想的差不多
02/02 03:15, 6F
→
02/02 03:16, 2年前 , 7F
全民公射 A很多0:射射平安
02/02 03:16, 7F
推
02/02 03:17, 2年前 , 8F
人民公設讚讚
02/02 03:17, 8F
→
02/02 03:23, 2年前 , 9F
沒有精液惹:00
02/02 03:23, 9F
推
02/02 03:26, 2年前 , 10F
什麼東西:00.. 窩猜跟弦論有關(X
02/02 03:26, 10F
→
02/02 03:26, 2年前 , 11F
關聯應該很遠:0
02/02 03:26, 11F
推
02/02 03:27, 2年前 , 12F
我學的量子物理怎麼沒教過
02/02 03:27, 12F
→
02/02 03:27, 2年前 , 13F
太苦了:000
02/02 03:27, 13F
→
02/02 03:34, 2年前 , 14F
這個會偏重量子計算:00
02/02 03:34, 14F
噓
02/02 05:58, 2年前 , 15F
尼寫U^(dagger) = U^(-1)就會變der比較好理解不少
02/02 05:58, 15F
‣ 更多 EliteMiko 的文章
文章代碼(AID): #1ZshYpr- (Marginalman)
討論串 (同標題文章)
完整討論串 (本文為第 4 之 6 篇)：
排序： 最新先 | 最舊先 | 留言數
在新視窗開啟完整討論串 (共6篇)
‣ 更多 EliteMiko 的文章
文章代碼(AID): #1ZshYpr- (Marginalman)