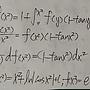看板 [ Math ]
討論串[微積] 一題微分方程求解
共 2 篇文章
內容預覽： 開啟 | 關閉 | 只限未讀
首頁
上一頁
1
下一頁
尾頁
#2
Re: [微積] 一題微分方程求解
推噓4(4推 0噓 11→)留言15則，0人參與, 6年前最新作者Vulpix (Sebastian)時間6年前 (2019/02/17 00:01), 6年前編輯資訊
0
1
0
內容預覽:
推文推得太累了，用回的整理一下。. 原題目中有一個積分方程：f(u) = 1 + ∫_0^u f(y)*( 1-tan(y) ) dy. (其中 u 代表原題目中的 x^2。). 顯然 f(0)=1。. 如果 f 和 tan 的解析性質夠好的話，f'(u) = f(u)*( 1-tan(u) )。.
(還有2235個字)
#1
[微積] 一題微分方程求解
推噓9(9推 0噓 41→)留言50則，0人參與, 6年前最新作者ac01965159 (leeleo)時間6年前 (2019/02/16 03:07), 編輯資訊
0
1
0
內容預覽:
題目如下圖，我看解答最後的f(x^2)=exp(x^2) * cos(x^2)，但是我算的如下圖，是f(x^2)=exp(x^2) * |cos(x^2)|，不知道為什麼解答不用加絕對值，因此最後的結果也差. 了一個負號。. https://i.imgur.com/ed98jIn.jpg. 謝謝版上
首頁
上一頁
1
下一頁
尾頁